【题目】
![]()
(1)写出数轴上A、B两点表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,t为何值时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
参考答案:
【答案】(1)-10;2;(2)t的值为4、5.2、5.5.
【解析】试题分析:(1)根据数轴上两点间的距离可得点A、点B所表示的数;
(2)一点恰好是另两点所连线段的中点有三种情况:
①若点O是点P与点Q的中点时,P、Q所表示的数互为相反数,列方程解得;
②若点P是点O与点Q的中点时,OQ=2OP,列方程解得;
③若点Q是点P与点O的中点时,OP=2OQ.列方程解得.
试题解析:(1)∵点C表示的数是6,BC=4,AB=12,且点A、点B在点C左边,
∴点B表示的数为:6-4=2,点A表示的数为:6-4-12=-10,
即数轴上A点表示的数为-10,数轴上B点表示的数为2;
(2)根据题意,t秒后点P表示的数为:-10+2t,点Q表示的数为:6-t,
有以下三种情况:
①若点O是点P与点Q的中点,则-10+2t+6-t=0,解得:t=4;
②若点P是点O与点Q的中点,则6-t=2(-10+2t),解得:t=5.2;
③若点Q是点P与点O的中点,则2(6-t)=-10+2t,解得:t=5.5;
综上,当t的值为4、5.2、5.5时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格线的交点叫格点,格点
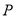 是
是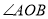 的边
的边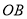 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).
(1)过点
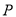 画
画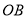 的垂线,交
的垂线,交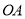 于点
于点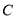 ;
;(2)线段 的长度是点O到PC的距离;
(3)
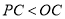 的理由是 ;
的理由是 ; (4)过点C画
 的平行线;
的平行线; -
科目: 来源: 题型:
查看答案和解析>>【题目】a
 b是新规定的一种运算法则:a
b是新规定的一种运算法则:a b=a2+ab,例如3
b=a2+ab,例如3 (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.(1)求(﹣3)
 5的值;
5的值;(2)若(﹣2)
 x=6,求x的值;
x=6,求x的值;(3)若3
 (2
(2 x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥DE,AC∥DF,AC=DF,添加下列条件,不能判断 △ABC≌△DEF的是( )
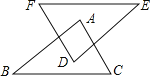
A. EF=BC B. AB=DE C. EF∥BC D.
 B=
B= E
E -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动。设点D,E的运动时间为t秒,DF⊥BC于F
(1)求证:AE=DF;
(2)如图2,连接EF,
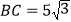
①是否存在t,使得四边形AEFD为菱形?若存在,求出t的值;若不存在,请说明理由
②连接DE,当△DEF是直角三角形时,求t的值
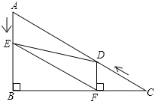
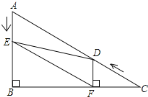
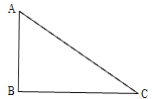

图1 图2 备用图 备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校允许学生在同个系列的校服里选择不同款式,新生入学后,学校就新生对校服款式选择情况作了抽样调查,调查分为款式A、B、C、D四种,每位新生只能选择一种款式,现将调查统计结果制成了如下两幅不完整的统计图,请结合这两幅统计图,回答下列问题:
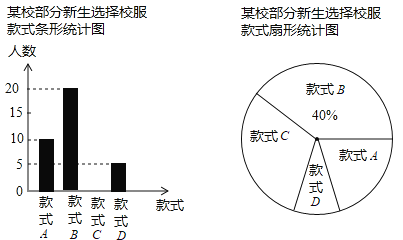
(1)在本次调查中,一共抽取了多少名新生,并补全条形统计图;
(2)若该校有847名新生,服装厂已生产了270套B款式的校服,请你按相关统计知识判断是否还要继续生产B款式的校服?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n
500
1000
1500
2000
2500
优等品频数m
471
946
1426
1898
2370
优等品频率
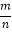
0.942
0.946
0.951
0.949
0.948
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图
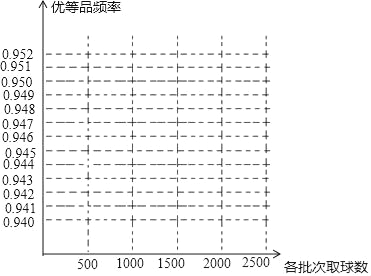
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为
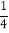 ,求取出了多少个黑球?
,求取出了多少个黑球?
相关试题

