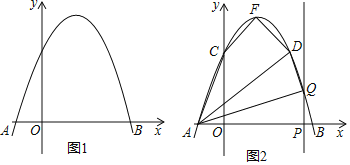
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
参考答案:
【答案】(1)y=﹣x2+2x+3;(2)①S四边形ACFD= 4;②Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
此题涉及的知识点是抛物线的综合应用,难度较大,需要有很好的逻辑思维,解题时先根据已知点的坐标列方程求出函数解析式,然后再根据解析式和已知条件求出四边形的面积和点的坐标。
(1)由题意可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴F(1,4),
∵C(0,3),D(2,3),
∴CD=2,且CD∥x轴,
∵A(﹣1,0),
∴S四边形ACFD=S△ACD+S△FCD=![]() ×2×3+
×2×3+![]() ×2×(4﹣3)=4;
×2×(4﹣3)=4;
②∵点P在线段AB上,
∴∠DAQ不可能为直角,
∴当△AQD为直角三角形时,有∠ADQ=90°或∠AQD=90°,
i.当∠ADQ=90°时,则DQ⊥AD,
∵A(﹣1,0),D(2,3),
∴直线AD解析式为y=x+1,
∴可设直线DQ解析式为y=﹣x+b′,
把D(2,3)代入可求得b′=5,
∴直线DQ解析式为y=﹣x+5,
联立直线DQ和抛物线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴Q(1,4);
ii.当∠AQD=90°时,设Q(t,﹣t2+2t+3),
设直线AQ的解析式为y=k1x+b1,
把A、Q坐标代入可得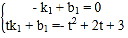 ,解得k1=﹣(t﹣3),
,解得k1=﹣(t﹣3),
设直线DQ解析式为y=k2x+b2,同理可求得k2=﹣t,
∵AQ⊥DQ,
∴k1k2=﹣1,即t(t﹣3)=﹣1,解得t=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
∴Q点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上可知Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求
 的长度.(结果保留π)
的长度.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C'处,连接C'D交AB于点E,连接BC',当△BC'D是直角三角形时,DE的长为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于A、B两点.
的图象交于A、B两点.(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
-
科目: 来源: 题型:
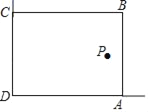
查看答案和解析>>【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为252m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
相关试题

