【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

参考答案:
【答案】(1)![]() 秒后△PCQ的面积为3平方厘米,此时PQ的长是
秒后△PCQ的面积为3平方厘米,此时PQ的长是![]() ;
;
(2)经过![]() 秒或
秒或![]() 秒,以A、B、P、Q为顶点的四边形的面积为22cm2
秒,以A、B、P、Q为顶点的四边形的面积为22cm2
【解析】试题分析:(1)根据题意∠C=90°,可以得出△PCQ的面积为![]() ×PC×CQ,设出t秒后满足要求,则根据△PCQ的面积是3 cm2列出等量关系求出t的值即可.
×PC×CQ,设出t秒后满足要求,则根据△PCQ的面积是3 cm2列出等量关系求出t的值即可.
(2)根据四边形ABQP的面积=SΔABC-SΔPCQ,列式计算即可.
试题解析:(1)设t秒后△PCQ的面积为3平方厘米,
则有PC=t cm,CQ=3t cm,
依题意,得: ![]() t×3t=3,
t×3t=3,
![]()
![]() (舍去)
(舍去)
由勾股定理,得:PQ=![]()
答: ![]() 秒后△PCQ的面积为3平方厘米,此时PQ的长是
秒后△PCQ的面积为3平方厘米,此时PQ的长是![]()
(2)① 当P在线段AC上,Q在线段BC上时, ![]()
S四边形APQB= S△ABC﹣S△PQC
![]()
![]() ,
,
得![]() (舍去)
(舍去)
② 当P在线段AC上,Q在线段BC延长线上时, ![]()
S四边形APBQ= S△AQC﹣S△PBC=![]()
![]() ,得
,得![]()
③ 当P在线段AC的延长线上,Q在线段BC延长线上时, ![]()
S四边形ABQP= S△PQC﹣S△ABC=![]()
![]() (不符合题意,舍去),(或者得
(不符合题意,舍去),(或者得![]() ,
, ![]() ,都不符合题意,舍去)
,都不符合题意,舍去)
综上: ![]() 或
或![]()
答,经过![]() 秒或
秒或![]() 秒,以A、B、P、Q为顶点的四边形的面积为22cm2
秒,以A、B、P、Q为顶点的四边形的面积为22cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是( )。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:
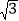 ≈1.73)
≈1.73)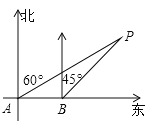
-
科目: 来源: 题型:
查看答案和解析>>【题目】聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)( )

A.169米 B.204米 C.240米 D.407米
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩
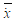 及其方差S2如表所示:
及其方差S2如表所示:甲
乙
丙
丁
(环)
8.4
8.6
8.6
7.6
S2
0.74
0.56
0.94
1.92
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好的开展“我爱阅读”活动,小明针对某校七年级学生(共16个班,480名学生)课外阅读喜欢图书的种类(每人只能选一种书籍)进行了调查.
(1)小明采取的下列调查方式中,比较合理的是 ;理由是: .
A.对七年级(1)班的全体同学进行问卷调查;
B.对七年级各班的语文科代表进行问卷调查;
C.对七年级各班学号为3的倍数的全体同学进行问卷调查.
(2)小明根据问卷调查的结果绘制了如下两幅不完整的统计图,根据图中提供的信息解答下列问题:
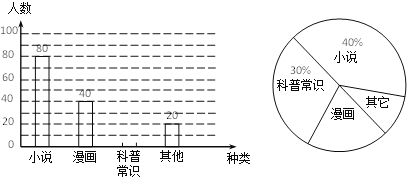
① 在扇形统计图中,“其它”所在的扇形的圆心角等于 度;
② 补全条形统计图;
③ 根据调查结果,估计七年级课外阅读喜欢“漫画”的同学有 人.
相关试题

