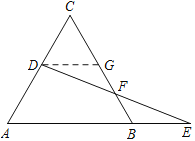
【题目】D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)如图1,求证:AD=DE;
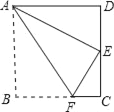
(2)如图2,DE交CB于点F.
①若DE⊥AC,CF=6,求BF的长;
②求证:DF=EF.

参考答案:
【答案】(1)证明见解析;(2)①3;②证明见解析
【解析】
(1)根据等边三角形的性质可得AB=AC,∠A=60°,由CD=BE,利用线段的和差关系可得AD=AE,即可证明△ADE是等边三角形,可得AD=DE;(2)①由DE⊥AC可得∠CFD=30°,根据含30°角的直角三角形的性质可求出CD的长,可得BE的长,根据∠BFE=∠CFD=30°,∠E=30°,可得BF=BE,即可得答案;②过点D作DG∥AB,交CB于点G,可得∠CGD=∠ABC=60°,∠GDF=∠E,由∠C=60°可证明△CDG是等边三角形,可得CD=DG,进而可得DG=BE,利用AAS可证明△GDF≌△BEF,即可得DF=EF.
(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵CD=BE,
∴AC=CD=AB-BE,即AD=AE,
∴△ADE是等边三角形,
∴AD=DE;
(2)①∵DF⊥AC,
∴∠CDF=90°,
∵∠C=60°,
在Rt△CDF中,∠CFD=30°,
∴CD=![]() CF=
CF=![]() ×6=3,
×6=3,
∵CD=BE,
∴BE=3,
∵∠BFE=∠CFD=30°,∠E=30°,
∴BE=BF,
∴BF=3;
②如图,过点D作DG∥AB,交CB于点G,
∴∠CGD=∠ABC=60°,∠GDF=∠E,
∵∠C=60°,
∴△CDG是等边三角形,
∴CD=DG,
∵CD=BE,
∴DG=BE,
在△GDF和△BEF中, ,
,
∴△GDF≌△BEF(AAS),
∴DF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12cm.
(1)求BC的长;
(2)分别连接OA,OB,OC,若△OBC的周长为26cm,求OA的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图,不写作法,保留作图痕迹
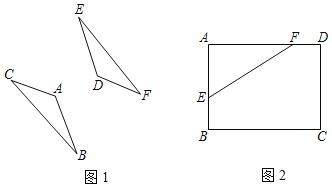
(1)如图1,若△ABC与△DEF关于直线l对称,请作出直线l;
(2)如图2,在矩形ABCD中,已知点B,F分别在AD和AB上,请在边BC上作出点G,在边CD作出点H,使得四边形FEGH的周长最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

-
科目: 来源: 题型:
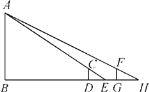
查看答案和解析>>【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时大华的影长GH=4 m如果大华的身高为2 m,求路灯杆AB的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
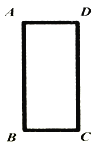
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求证:平行四边形ABCD是矩形;
(2)求BF的长;
(3)求折痕AF长.
相关试题

