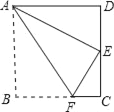
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求证:平行四边形ABCD是矩形;
(2)求BF的长;
(3)求折痕AF长.
参考答案:
【答案】(1)见解析;(2)5cm;(3)5![]() cm.
cm.
【解析】分析:(1)根据翻折变换的对称性可知AE=AB,在△ADE中,利用勾股定理逆定理证明三角形为直角三角形,再根据有一个角是直角的平行四边形是矩形证明即可;
(2)设BF为x,分别表示出EF、EC、FC,然后在△EFC中利用勾股定理列式进行计算即可;
(3)在Rt△ABF中,利用勾股定理求解即可.
详解:(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,
∴AE=AB=10,AE2=102=100,
又∵AD2+DE2=82+62=100,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,且∠D=90°,
又∵四边形ABCD为平行四边形,
∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);
(2)设BF=x,则EF=BF=x,EC=CD-DE=10-6=4cm,FC=BC-BF=8-x,
在Rt△EFC中,EC2+FC2=EF2,
即42+(8-x)2=x2,
解得x=5,
故BF=5cm;
(3)在Rt△ABF中,由勾股定理得,AB2+BF2=AF2,
∵AB=10cm,BF=5cm,
∴AF=![]() =5
=5![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)如图1,求证:AD=DE;
(2)如图2,DE交CB于点F.
①若DE⊥AC,CF=6,求BF的长;
②求证:DF=EF.

-
科目: 来源: 题型:
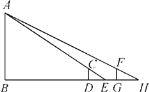
查看答案和解析>>【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时大华的影长GH=4 m如果大华的身高为2 m,求路灯杆AB的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
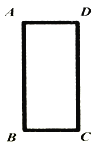
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DB∥AC,且DB=
 AC,E是AC的中点.
AC,E是AC的中点.(1)求证:BC=DE;
(2)连接AD、BE,若∠BAC=∠C,求证:四边形DBEA是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】20、如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)填空:点A关于X轴对称的点的坐标是 ___,点B关于Y轴对称的点的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等边△ABC中,点D.E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE
(2)求∠DFC的度数

相关试题

