【题目】已知,直线![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,且点
,且点![]() 的横坐标为4,过
的横坐标为4,过![]() 轴上一点
轴上一点![]() 作
作![]() 垂直于
垂直于![]() 交
交![]() 于
于![]() 点,如图.
点,如图.

(1)若点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() ,
,![]() ,垂足分别于
,垂足分别于![]() 、
、![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
(2)在(1)的![]() 取得最小值的前提下,将
取得最小值的前提下,将![]() 沿射线
沿射线![]() 平移,记平移后的三角形为
平移,记平移后的三角形为![]() ,当
,当![]() 时,在平面内存在点
时,在平面内存在点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点构成平行四边形,这样的点
四点构成平行四边形,这样的点![]() 有几个?直接写出点
有几个?直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() 最小值为4.8;(2)这样的
最小值为4.8;(2)这样的![]() 点有3个,
点有3个,![]() ;
;![]() ;
;![]() .
.
【解析】
(1)利用反比例函数图象上点的坐标特征可求出点A的坐标,由点A的坐标,利用待定系数法可求出直线0A的解析式,设点P的坐标为(m,![]() m)(
m)(![]() ),则PE=
),则PE=![]() m,PF=8-m,利用勾股定理可找出EF2关于m的函数关系式,再利用二次函数的性质,即可求出EF2的最小值,进而可得出段EF长度的最小值;
m,PF=8-m,利用勾股定理可找出EF2关于m的函数关系式,再利用二次函数的性质,即可求出EF2的最小值,进而可得出段EF长度的最小值;
(2)由(1)的结论结合平移的性质,可得出平移后点![]() 、
、![]() 、
、![]() 的坐标.
的坐标.
解:(1)当x=4时,![]()
∴![]()
设直线OA的解析式为![]()
将![]() 代入
代入![]() 得k=
得k=![]()
设点P的坐标为(m,![]() m)(
m)(![]() ) 则PE=
) 则PE=![]() m,PF=8-m
m,PF=8-m
∴FE2=PF2+PE2即FE2=(![]() m)2+(8-m)2=
m)2+(8-m)2=![]() (m-
(m-![]() )2+
)2+![]()
![]()
∴当m=![]() 时,EF2取得最小值,此时EF最小值为
时,EF2取得最小值,此时EF最小值为![]()
∴![]() 最小值为4.8.
最小值为4.8.
(2)这样的![]() 点有3个.
点有3个.
![]() ;
;![]() ;
;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】将1,2,3,...,30,这30个整数,任意分为15组,每组2个数.现将每组数中的一个数记为
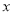 ,另一个数记为
,另一个数记为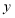 ,计算代数式
,计算代数式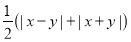 的值,15组数代入后可得到15个值,则这15个值之和的最小值为( )
的值,15组数代入后可得到15个值,则这15个值之和的最小值为( )A.
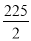 B.120C.225D.240
B.120C.225D.240 -
科目: 来源: 题型:
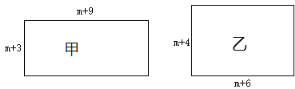
查看答案和解析>>【题目】有甲、乙两个长方形纸片,边长如图所示
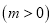 ,面积分别为
,面积分别为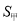 和
和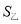 .
.
(1)①计算:
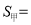 ______,
______,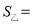 ______;
______;②用“<”“=”或“>”填空:
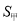 ______
______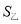
(2)若一个正方形纸片的周长与乙长方形的周长相等,面积为
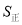 .
.①该正方形的边长是______(用含
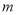 的代数式表示);
的代数式表示);②小方同学发现:
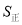 与
与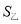 的差与
的差与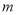 无关.请判断小方的发现是否正确,并通过计算说明你的理由.
无关.请判断小方的发现是否正确,并通过计算说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
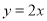 的图象与反比例函数
的图象与反比例函数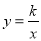 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.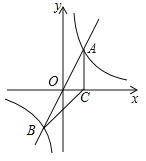
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应“弘扬传统文化”的号召,万州区某中学举行了一次中学生诗词大赛活动.小何同学对他所在八年级一班参加诗词大赛活动同学的成绩进行了整理,成绩分别100分、90分、80分、70分,并绘制出如下的统计图.
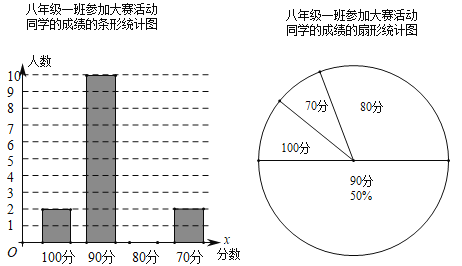
请根据以上提供的信息,解答下列问题:
(1)该校八年级(1)班参加诗词大赛成绩的众数为______分;并补全条形统计图.
(2)求该校八年级(1)班参加诗词大赛同学成绩的平均数;
(3)结合平时成绩、期中成绩和班级预选成绩(如下表),年级拟从该班小何和小王的两位同学中选一名学生参加区级决赛,按
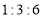 的比例计算两位同学的最终得分,请你根据计算结果确定选谁参加区级决赛.
的比例计算两位同学的最终得分,请你根据计算结果确定选谁参加区级决赛.学生姓名
平时成绩
期中成绩
预选成绩
小何
80
90
100
小王
90
100
90
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2﹣
 x+c与x轴相交于A、B两点,并与直线y=
x+c与x轴相交于A、B两点,并与直线y= x﹣2交于B、C两点,其中点C是直线y=
x﹣2交于B、C两点,其中点C是直线y= x﹣2与y轴的交点,连接AC.
x﹣2与y轴的交点,连接AC.(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
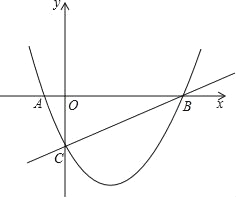
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级为庆祝中华人民共和国建国70周年,准备举行唱红歌、颂经典活动.八年级(2)班积极准备,需购买文件夹若干,某文具店有甲、乙两种文件夹.
(1)若该班只购买甲种文件夹,且购买甲种文件夹的花费
 (单位:元)与其购买数量
(单位:元)与其购买数量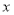 (单位:件)满足一次函数关系,若购买20个,需花费180元;若购买30个,需花费260元.该班若需购买甲种文件夹60件,求需花费多少元?
(单位:件)满足一次函数关系,若购买20个,需花费180元;若购买30个,需花费260元.该班若需购买甲种文件夹60件,求需花费多少元?(2)若该班购买甲,乙两种文件夹,那么甲种文件夹的单价比乙种文件夹的单价贵2元,若用240元购买甲种文件夹的数量与用180元购买乙种文件夹的数量相同.求该文具店甲乙两种文件夹的单价分别是多少元?
相关试题

