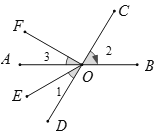
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是_____ _____(把符合条件的角都填出来);
(2)如果∠AOC=120°,那么根据____ ______,可得∠BOD=__________°;
(3)如果∠1=32°,求∠2和∠3的度数.
参考答案:
【答案】(1)∠AOD,∠BOC;(2)对顶角相等;120°;(3)∠2=64°,∠3=26°.
【解析】
(1)由垂线的定义和角的互余关系即可得出结果;
(2)由对顶角相等即可得出结果;
(3)由角平分线的定义求出∠AOD,由对顶角相等得出∠2的度数,再由角的互余关系即可求出∠3的度数.
(1)∵直线AB,CD相交于点O,
∴∠AOD=∠BOC
∵OF⊥OC
∴∠COF=90°
∴∠AOF+∠2=90°
∴∠AOF+∠AOD=90°
∠AOF的余角是∠2和∠AOD.即∠AOF的余角是∠BOC和∠AOD
(2)如果∠AOC=120°,那么根据对顶角相等可得∠BOD=120°
(3)∵OE平分∠AOD,∴∠AOD=2∠1=2×32°=64°
∴∠2=∠AOD=64°
∵∠COF=90°
∴∠3=90°-∠2=90°-64°=26°.
-
科目: 来源: 题型:
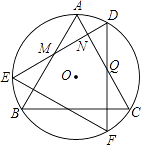
查看答案和解析>>【题目】如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 ①②③ .(把所有正确的结论的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.

(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值. -
科目: 来源: 题型:
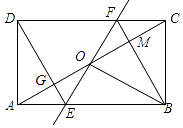
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件成本10元,试销阶段每件产品的销售单价x(元/件)与日销售量y(件)之间的关系如下表.
x(元∕件)
15
18
20
22
…
y(件)
250
220
200
180
…
按照这样的规律可得,日销售利润w(元)与销售单价x(元/件)之间的函数关系式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是 .
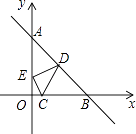
-
科目: 来源: 题型:
查看答案和解析>>【题目】用圆规、直尺作图,不写作法,但到保留作图痕迹.
已知:线段a,
求作:正方形ABCD,使其对角线AC=a.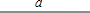
相关试题

