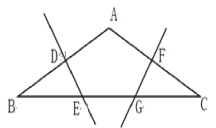
【题目】如图,AB=AC,∠A=120,BC=6cm,ED、FG分别是AB,AC的垂直平分线,求BE的长.
参考答案:
【答案】BE=2cm.
【解析】
连接AE、AG,根据等腰三角形的性质可得:∠B=∠C=30°,然后根据垂直平分线的性质可得:BE=AE,AG=CG,从而得出:∠B=∠BAE=30°,∠C=∠CAG=30°,然后根据三角形外角的性质可得:∠AEG=∠AGE=60°,再根据等边三角形的判定可得:△AEG是等边三角形,从而得出:AE=EG=AG,即可求出BE= EG= CG =2cm.
解:连接AE、AG,

∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE、FG分别为线段AB、AC的垂直平分线,
∴BE=AE,AG=CG,
∴∠B=∠BAE=30°,∠C=∠CAG=30°,
∵∠AEG与∠AGE分别是△AEB与△AGC的外角,
∴∠AEG=∠B+∠BAE=30°+30°=60°,∠AGE=∠C+∠CAG=30°+30°=60°,
∴△AEG是等边三角形,
∴AE=EG=AG,
∵BE=AE,AG=CG,BC=6cm,
∴BE= EG= CG =2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点 在边
在边 上,且
上,且 ,点
,点 为
为 的中点,点
的中点,点 为边
为边 上的动点,当点
上的动点,当点 在
在 上移动时,使四边形
上移动时,使四边形 周长最小的点
周长最小的点 的坐标为( )
的坐标为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
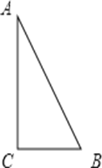
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
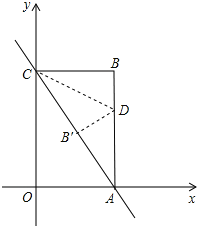
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】飞镖随机地掷在下面的靶子上.
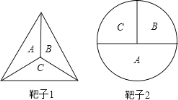
 在每一个靶子中,飞镖投到区域
在每一个靶子中,飞镖投到区域 、
、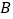 、
、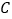 的概率是多少?
的概率是多少? 在靶子
在靶子 中,飞镖投在区域
中,飞镖投在区域 或
或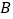 中的概率是多少?
中的概率是多少?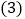 在靶子
在靶子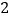 中,飞镖没有投在区域
中,飞镖没有投在区域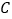 中的概率是多少?
中的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

相关试题

