【题目】如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
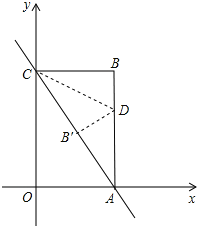
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(4,0),C(0,8);(2)y=﹣![]() x+8;(3)满足条件的点P有三个,分别为:(0,0),(
x+8;(3)满足条件的点P有三个,分别为:(0,0),(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ).
).
【解析】
试题分析:(1)已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,即可求得A和C的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,最后即可求出CD的解析式;
(3)将点P在不同象限进行分类,根据全等三角形的判定方法找出所有全等三角形,找出符合题意的点P的坐标.
解:(1)令y=0,则﹣2x+8=0,解得x=4,
∴A(4,0),
令x=0,则y=8,
∴C(0,8);
(2)由折叠可知:CD=AD,
设AD=x,则CD=x,BD=8﹣x,
由题意得,(8﹣x)2+42=x2,
解得x=5,
此时AD=5,
∴D(4,5),
设直线CD为y=kx+8,
把D(4,5)代入得5=4k+8,解得k=﹣![]() ,
,
∴直线CD的解析式为y=﹣![]() x+8;
x+8;
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图1,
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD=5,AP=BC=4,PD=BD=8﹣5=3,
由AD×PQ=DP×AP得:5PQ=3×4,
∴PQ=![]() ,
,
∴xP=4+![]() =
=![]() ,把x=
,把x=![]() 代入y=﹣
代入y=﹣![]() x+8得y=
x+8得y=![]() ,
,
此时P(![]() ,
,![]() )
)
③当点P在第二象限时,如图2,
同理可求得:PQ=![]() ,
,
在RT△PCQ中,CQ=![]() =
=![]() =
=![]() ,
,
∴OQ=8﹣![]() =
=![]() ,
,
此时P(﹣![]() ,
,![]() ),
),
综上,满足条件的点P有三个,分别为:(0,0),(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ).
).


-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
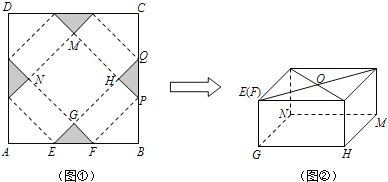
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a+4b=7ab B.(ab3)3=ab6 C.(a+2)2=a2+4 D.x12÷x6=x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为20 (元/个)的计算器,其销售量y (万个)与销售价格x (元/个)之间为一次函数关系,其变化如下表:
价格x (元/个)
…
30
50
…
销售量y (万个)
…
5
3
…
同时,销售过程中的其他开支(不含进价)总计40万元.若该公司要获得40万元的净利润,且尽可能让顾客得到实惠,那么销售价格应定为多少?
(注:净利润=总销售额﹣总进价﹣其他开支)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.

(1)求∠BDC的度数.
(2)求AC的长度.
相关试题

