【题目】阅读下面材料,回答问题
距离能够产生美.
唐代著名文学家韩愈曾赋诗:“天街小雨润如酥,草色遥看近却无.
当代印度著名诗人泰戈尔在《世界上最遥远的距离》中写道:
“世界上最遥远的距离
不是瞬间便无处寻觅
而是尚未相遇
便注定无法相聚”
距离是数学、天文学、物理学中的热门话题,唯有对宇宙距离进行测量,人类才能掌握世界尺度.
已知点 A,B 在数轴上分别表示有理数 a,b,A,B 两点之间的距离表示为 AB.
(![]() )当 A,B 两点中有一点在原点时,不妨设点 A 在原点,如图 1,
)当 A,B 两点中有一点在原点时,不妨设点 A 在原点,如图 1,![]() .
.
(![]() )当 A,B 两点都不在原点时,
)当 A,B 两点都不在原点时,
①如图 2,点 A,B 都在原点的右边,![]() ;
;
②如图 3,点 A,B 都在原点的左边,![]() ;
;
③如图 4,点 A,B 在原点的两边,![]() .
.
综上,数轴上 A,B 两点的距离 ![]() .
.
利用上述结论,回答以下三个问题:
![]()
(1)若数轴上表示 ![]() 和
和![]() 的两点之间的距离是
的两点之间的距离是![]() ,则
,则 ![]() ;
;
(2)若代数式 ![]() 取最小值时,则
取最小值时,则![]() 的取值范围是 ;
的取值范围是 ;
(3)若未知数 ![]() ,
,![]() 满足
满足 ![]() ,则代数式
,则代数式 ![]() 的最大值是 ,最小值是 .
的最大值是 ,最小值是 .
参考答案:
【答案】(1)-6或2;(2)-1≤x≤2;(3)7,-1;
【解析】
(1)把问题转化为绝对值方程,即可解决问题.
(2)若代数式|x+1|+|x-2|取最小值时,表示在数轴上找一点x,到-1和2的距离之和最小,显然这个点x在-1和2之间(包括-1,2),由此即可解决问题.
(3))因为(|x-1|+|x-3|)(|y-2|+|y+1|)=6,又因为|x-1|+|x-3|的最小值为2,|y-2|+|y+1|的最小值为3,所以1≤x≤3,-1≤y≤2,由此不难得到答案.
(1)若数轴上表示x和-2的两点之间的距离是4,
则|x+2|=4,
解得x=-2-4=-6或x=-2+4=2.
故答案为-6或2.
(2)若代数式|x+1|+|x-2|取最小值时,表示在数轴上找一点x,到-1和2的距离之和最小,显然这个点x在-1和2之间(包括-1,2),
∴x的取值范围是-1≤x≤2,
故答案为-1≤x≤2.
(3)∵(|x-1|+|x-3|)(|y-2|+|y+1|)=6,
又∵|x-1|+|x-3|的最小值为2,|y-2|+|y+1|的最小值为3,
∴1≤x≤3,-1≤y≤2,
∴代数式x+2y的最大值是7,最小值是-1.
故答案为7,-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.

-
科目: 来源: 题型:
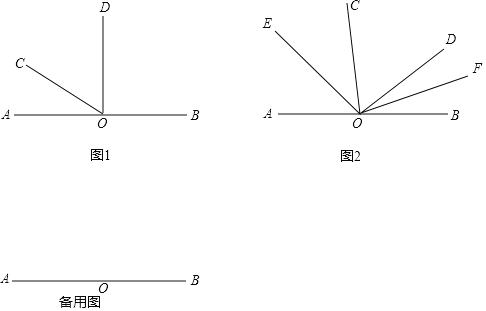
查看答案和解析>>【题目】已知:如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角时,3∠AOC=∠BOD,求∠COD的度数;
(2)若∠COD保持在(1)中的大小不变,它绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)若∠COD从(1)中的位置开始,边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转(当其中一边与OB重合时都停止旋转),OM、ON分别平分∠BOC、∠BOD.
求:①运动多少秒后,∠COD=10°;
②运动多少秒后,∠COM=∠BON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC

(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于
 ;
;②连OD,在OD上画出点P,使OP得长等于
 ,请写出画法,并说明理由.
,请写出画法,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
相关试题

