【题目】如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.

参考答案:
【答案】证明见解析.
【解析】试题分析:要想证明△DBE是等腰三角形,只需证明∠BED与∠D相等即可,∠FEC与∠BED是对顶角,只需证∠FEC与∠D相等即可,而由DF⊥AC可得∠C+∠FEC=90°,∠A+∠D=90°,因此只需证∠A=∠C,要想证明∠A=∠C,需证AB=BC,AB=BC 是已知,从而问题得证.
试题解析:在△ABC中,BA=BC,
∵BA=BC,∴∠A=∠C,∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°,∴∠FEC=∠D,
∵∠FEC=∠BED,∴∠BED=∠D,∴BD=BE,即△DBE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乳品公司最近推出一款果味酸奶,共有红枣、木瓜两种口味,若送奶员连续三天,每天从中任选一瓶某种口味的酸奶赠送给某住户品尝,则该住户收到的三瓶酸奶中,至少有两瓶为红枣口味的概率是多少?
(请用“画树状图”的方法给出分析过程,并求出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.
(I)请填写下表
购买量/kg
0
50
100
150
200
…
付款金额/元
0
250
_
700
__
…
(Ⅱ)写出付款金额关于购买量的函数解析式;
(Ⅲ)如果某人付款2100元,求其购买苹果的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证:
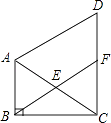
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?商品名
单价(元)
数量(个)
金额(元)
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计
8
28
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠ABC=90,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D.E.F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是( )
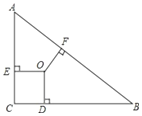
A. 2,2,2 B. 3,3,3 C. 4,4,4 D. 5,5,5
相关试题

