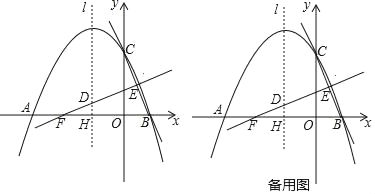
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C(0,4),线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x轴交于点H.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R.求点P的坐标;
(4)点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M.N为顶点的四边形是平行四边形?若存在,则直接写出N点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线表达式为:y=﹣![]() (x+4)(x﹣2)=﹣
(x+4)(x﹣2)=﹣![]() x2﹣x+4;(2)点D坐标为(﹣1,1);(3)点P坐标为(
x2﹣x+4;(2)点D坐标为(﹣1,1);(3)点P坐标为(![]() ,0)或(7,0);(4)存在(﹣1,
,0)或(7,0);(4)存在(﹣1,![]() )、(﹣1,
)、(﹣1,![]() )、(﹣1,﹣
)、(﹣1,﹣![]() )
)
【解析】(1)利用待定系数法问题可解;
(2)依据垂直平分线性质,利用勾股定理构造方程;
(3)由题意画示意图可以发现由两种可能性,确定方案后利用锐角三角函数定义构造方程,求出半径及点P坐标;
(4)通过分类讨论画出可能图形,注意利用平行四边形的性质,同一对角线上的两个端点到另一对角线距离相等.
(1)∵抛物线过点A(﹣4,0),B(2,0)
∴设抛物线表达式为:y=a(x+4)(x﹣2)
把C(0,4)带入得
4=a(0+4)(0﹣2)
∴a=﹣![]() ,
,
∴抛物线表达式为:y=﹣![]() (x+4)(x﹣2)=﹣
(x+4)(x﹣2)=﹣![]() x2﹣x+4
x2﹣x+4
(2)由(1)抛物线对称轴为直线x=﹣![]() =﹣1,
=﹣1,
∵线段BC的中垂线与对称轴l交于点D,
∴点D在对称轴上,
设点D坐标为(﹣1,m),
过点C做CG⊥l于G,连DC,DB,

∴DC=DB,
在Rt△DCG和Rt△DBH中
∵DC2=12+(4﹣m)2,DB2=m2+(2+1)2
∴12+(4﹣m)2=m2+(2+1)2
解得:m=1
∴点D坐标为(﹣1,1);
(3)∵点B坐标为(2,0),C点坐标为(0,4)
∴BC=![]() ,
,
∵EF为BC中垂线
∴BE=![]()
在Rt△BEF和Rt△BOC中,
cos∠CBF=![]() ,
,
∴![]() ,
,
∴BF=5,EF=![]() ,OF=3
,OF=3
设⊙P的半径为r,⊙P与直线BC和EF都相切,
如图:

①当圆心P1在直线BC左侧时,连P1Q1,P1R1,则P1Q1=P1R1=r1
∴∠P1Q1E=∠P1R1E=∠R1EQ1=90°
∴四边形P1Q1ER1是正方形
∴ER1=P1Q1=r1
在Rt△BEF和Rt△FR1P1中
tan∠1=![]() ,
,
∴![]() ,
,
∴r1=![]() ,
,
∵sin∠1=![]() ,
,
∴FP1=![]() ,OP1=
,OP1=![]() ,
,
∴点P1坐标为(![]() ,0)
,0)
②同理,当圆心P2在直线BC右侧时,
可求r2=![]() ,OP2=7
,OP2=7
∴P2坐标为(7,0)
∴点P坐标为(![]() ,0)或(7,0)
,0)或(7,0)
(4)存在,
当点P坐标为(![]() ,0)时,
,0)时,
①若DN和MP为平行四边形对边,则有DN=MP
当x=![]() 时,y=﹣
时,y=﹣![]() ,
,
∴DN=MP=![]()
∴点N坐标为(﹣1,![]() )
)
②若MN、DP为平行四边形对边时,M、P点到ND距离相等
则点M横坐标为﹣![]()
则M纵坐标为﹣![]() ,
,
由平行四边形中心对称性可知,点M到N的垂直距离等于点P到点D的垂直距离,
当点N在D点上方时,点N纵坐标为![]() ,
,
此时点N坐标为(﹣1,![]() ),
),
当点N在x轴下方时,点N坐标为(﹣1,﹣![]() ),
),
当点P坐标为(7,0)时,所求N点不存在.
故答案为:(﹣1,![]() )、(﹣1,
)、(﹣1,![]() )、(﹣1,﹣
)、(﹣1,﹣![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.
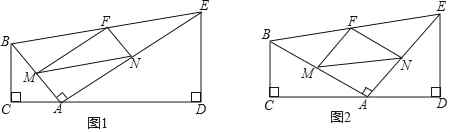
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求
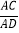 的值;
的值;(2)若tan∠FMN=
 ,BC=4,则可求出图中哪些线段的长?写出解答过程;
,BC=4,则可求出图中哪些线段的长?写出解答过程;(3)连接CM,DN,CF,DF.试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC,BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件是( )

A. AD=BC
B. AC=BD
C. AB=CD
D. AD=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设有理数a、b、c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x﹣
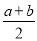 |+|x﹣
|+|x﹣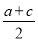 |+|x+
|+|x+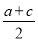 |的最小值是( )
|的最小值是( )A.
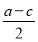 B.
B.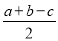 C.
C.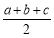 D.
D.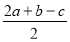
-
科目: 来源: 题型:
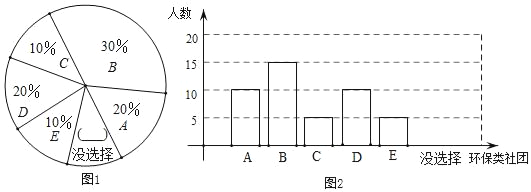
查看答案和解析>>【题目】某校创建“环保示范学校”,为了解全校学生参加环保类杜团的意愿,在全校随机抽取了50名学生进行问卷调查,问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如表:
社团名称
A.酵素制作社团
B.回收材料小制作社团
C.垃圾分类社团
D.环保义工社团
E.绿植养护社团
人数
10
15
5
10
5
(1)填空:在统计表中,这5个数的中位数是 ;
(2)根据以上信息,补全扇形图(图1)和条形图(图2);
(3)该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(4)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.
相关试题

