【题目】某校创建“环保示范学校”,为了解全校学生参加环保类杜团的意愿,在全校随机抽取了50名学生进行问卷调查,问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如表:
社团名称 | A.酵素制作社团 | B.回收材料小制作社团 | C.垃圾分类社团 | D.环保义工社团 | E.绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
(1)填空:在统计表中,这5个数的中位数是 ;
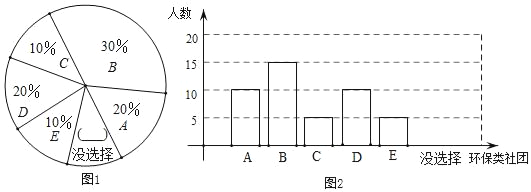
(2)根据以上信息,补全扇形图(图1)和条形图(图2);
(3)该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(4)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.
参考答案:
【答案】(1)10;(2)补图见解析;(3)280名;(4)![]()
【解析】(1)根据中位数的定义即可判断;
(2)求出没有选择的百分比,高度和E相同,即可画出图形;
(3)利用样本估计总体的思想解决问题即可;
(4)画出树状图即可解决问题;
(1)这5个数从小到大排列:5,5,10,10,15,故中位数为10,
故答案为10.
(2)没有选择的占1﹣10%﹣30%﹣20%﹣10%﹣20%=10%,
条形图的高度和E相同;如图所示:
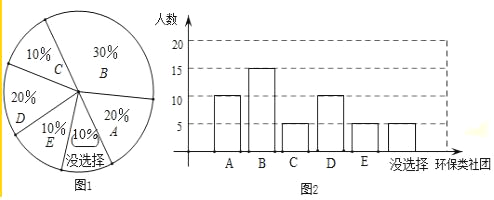
(3)1400×20%=280(名)
答:估计全校有多少学生愿意参加环保义工社团有280名;
(4)酵素制作社团、绿植养护社团分别用A、B表示:树状图如图所示,
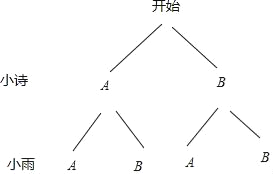
共有4种可能,两人同时选择绿植养护社团只有一种情形,
∴这两名同学同时选择绿植养护社团的概率=![]() .
.
-
科目: 来源: 题型:
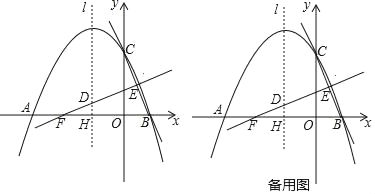
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C(0,4),线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x轴交于点H.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R.求点P的坐标;
(4)点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M.N为顶点的四边形是平行四边形?若存在,则直接写出N点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设有理数a、b、c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x﹣
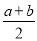 |+|x﹣
|+|x﹣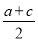 |+|x+
|+|x+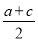 |的最小值是( )
|的最小值是( )A.
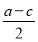 B.
B.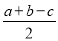 C.
C.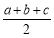 D.
D.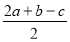
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读思考,完成下列填空.
问题提出:
如图,图①是一张由三个边长为1的小正方形组成的
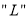 形纸片.图②是张
形纸片.图②是张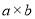 的方格纸(
的方格纸(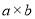 的方格纸指边长分别为
的方格纸指边长分别为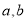 的长方形,被分成
的长方形,被分成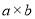 个边长为1的小正方形,其中
个边长为1的小正方形,其中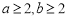 ,且
,且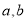 为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?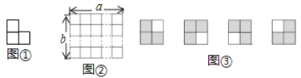
问题探究;
探究一:把图①放置在
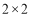 的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.探究二:把图①放置在
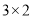 的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在
的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在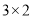 的方格纸中,共可以找到2个位置不同的
的方格纸中,共可以找到2个位置不同的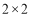 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在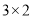 的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.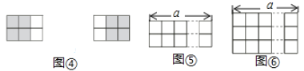
探究三:把图①放置在
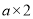 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在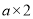 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的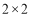 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在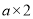 的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.探究四:把图①放置在
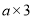 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在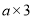 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的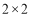 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在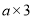 的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.……
问题解决:
把图①放置在
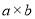 的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法. -
科目: 来源: 题型:
查看答案和解析>>【题目】点
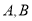 为数轴上的两点,点
为数轴上的两点,点 对应的数为
对应的数为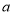 ,点
,点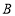 对应的数为3,
对应的数为3,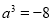 .
.(1)求
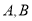 两点之间的距离;
两点之间的距离;(2)若点
 为数轴上的一个动点,其对应的数记为
为数轴上的一个动点,其对应的数记为 ,试猜想当
,试猜想当 满足什么条件时,点
满足什么条件时,点 到
到 点的距离与点
点的距离与点 到
到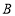 点的距离之和最小.请写出你的猜想,并说明理由:
点的距离之和最小.请写出你的猜想,并说明理由:(3)若
 为数轴上的两个动点(
为数轴上的两个动点(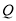 点在
点在 点右侧),
点右侧),  两点之间的距离为
两点之间的距离为 ,当点
,当点 到A点的距离与点
到A点的距离与点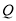 到
到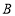 点的距离之和有最小值4时,
点的距离之和有最小值4时, 的值为_________.
的值为_________.
相关试题

