【题目】如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件是( )

A. AD=BC
B. AC=BD
C. AB=CD
D. AD=CD
参考答案:
【答案】A
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AD且EF=![]() AD,同理可得GH∥AD且GH=
AD,同理可得GH∥AD且GH=![]() AD,EH∥BC且EH=
AD,EH∥BC且EH=![]() BC,然后证明四边形EFGH是平行四边形,再根据邻边相等的平行四边形是菱形解答.
BC,然后证明四边形EFGH是平行四边形,再根据邻边相等的平行四边形是菱形解答.
解:应满足AD=BC.
理由如下:∵E,F分别是AB,BD的中点,
∴EF∥AD且EF=![]() AD,同理可得:GH∥AD且GH=
AD,同理可得:GH∥AD且GH=![]() AD,EH∥BC且EH=
AD,EH∥BC且EH=![]() BC,
BC,
∴EF∥GH且EF=GH,
∴四边形EFGH是平行四边形,
∵AD=BC,
∴![]() AD=
AD=![]() BC,即EF=EH,
BC,即EF=EH,
∴平行四边形EFGH是菱形.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的 ;
;(2)问两动点经过多长时间使得点P与点Q之间的距离为
 ?若存在,
?若存在,求出运动所需的时间;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.
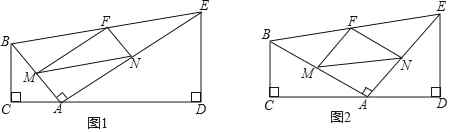
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求
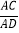 的值;
的值;(2)若tan∠FMN=
 ,BC=4,则可求出图中哪些线段的长?写出解答过程;
,BC=4,则可求出图中哪些线段的长?写出解答过程;(3)连接CM,DN,CF,DF.试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC,BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
-
科目: 来源: 题型:
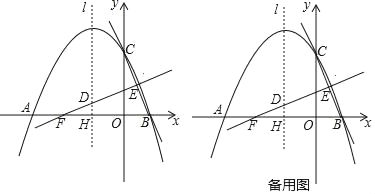
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C(0,4),线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x轴交于点H.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R.求点P的坐标;
(4)点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M.N为顶点的四边形是平行四边形?若存在,则直接写出N点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设有理数a、b、c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x﹣
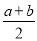 |+|x﹣
|+|x﹣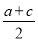 |+|x+
|+|x+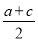 |的最小值是( )
|的最小值是( )A.
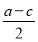 B.
B.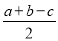 C.
C.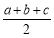 D.
D.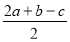
相关试题

