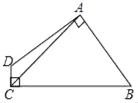
【题目】如图，在山顶上有一座电视塔，在塔顶B处，测得地面上一点A的俯角α=60°，在塔底C处测得的俯角β=45°，已知BC=60m，求山高CD（精确到1m， ≈1.732）

参考答案：

【答案】解：设山高CD=x（米），

∵∠CAD=∠β=45°，∠BAD=∠α=60°，∠ADB=90°，

∴AD=CD=x，BD=ADtan60°= x．

∵BD﹣CD=BC=60，

∴ x﹣x=60．

∴x= =30（ +1）．

∴CD=30×（1.732+1）≈82（米）．

答：山高CD约为82米．


【解析】抓住题中关键的已知条件，得出∠CAD和∠BAD的度数，从而可得出AD=CD=x，则根据解直角三角形，可表示出BD的长，再根据BD﹣CD=BC=60，建立关于x的方程，求解即可。
【考点精析】本题主要考查了解一元一次方程的步骤和解直角三角形的相关知识点，需要掌握先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．

关闭