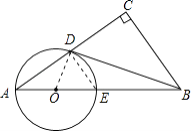
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE= ![]() :
: ![]() ,BC=6,求切线BD的长.
,BC=6,求切线BD的长.
参考答案:
【答案】
(1)证明:连接OD
∵OA=OD,
∴∠A=∠ADO(等边对等角).
又∵∠A+∠CDB=90°(已知),
∴∠ADO+∠CDB=90°(等量代换),
∴∠ODB=180°﹣(∠ADO+∠CDB)=90°,即BD⊥OD.
又∵OD是圆O的半径.
∴BD是⊙O切线
(2)解:连接DE,则∠ADE=90°(圆周角定理).
∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
又∵D是AC中点,
∴DE是△ABC的中位线,
∴DE= ![]() BC=3,AE=BE.
BC=3,AE=BE.
∵AD:AE= ![]() :
: ![]() ,
,
在直角△ADE中,利用勾股定理求得AE=3 ![]() ,则AB=6
,则AB=6 ![]() .
.
∴BD2=ABBE=6 ![]() ×3
×3 ![]() =54,
=54,
∴BD=3 ![]() .
.
【解析】(1)要证明BD是⊙O切线,由题意可知点D在圆上,因此连接OD,需证OD⊥BD,就要证∠ODB=90°,根据已知易证∠ADO+∠CDB=90°,即可证得结论
(2)先证明DE∥BC,由D是AC中点,可证得DE是△ABC的中位线,即可求得DE的长,再根据AD与AE的比值及勾股定理,就可以求得AE、AB的长,然后根据切割线定理得出BD2=ABBE,从而可求得BD的长。
【考点精析】掌握勾股定理的概念和三角形中位线定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为m(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知AB=6cm,BC=10cm.则EC的长为_____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明解不等式
 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程ax2+2x﹣1=0.
(1)若该方程无解,求a的取值范围;
(2)当a=1时,求该方程的解. -
科目: 来源: 题型:
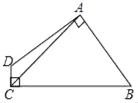
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,
 ≈1.732)
≈1.732)
相关试题

