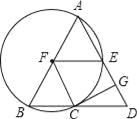
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.
参考答案:
【答案】证明见解析(2)60(3)30°
【解析】试题分析:(1)由等腰三角形的性质得出∠D=∠BCF,证出CF∥AD,由已知条件得出CG⊥CF,即可得出结论;
(2)①根据平行线的性质得出△BCF∽△BDA,得出![]() ,△BCF的面积:△BDA的面积=1:4,即可得出结果;
,△BCF的面积:△BDA的面积=1:4,即可得出结果;
②证出△BCF是等边三角形,得出∠B=60°,CF=BF=![]() AB,证出△ABD是等边三角形,CF=
AB,证出△ABD是等边三角形,CF=![]() AD,证出△AEF是等边三角形,得出AE=AF=
AD,证出△AEF是等边三角形,得出AE=AF=![]() AB=
AB=![]() AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
试题解析:(1)∵AB=AD,FB=FC,
∴∠B=∠D,∠B=∠BCF,
∴∠D=∠BCF,
∴CF∥AD,
∵CG⊥AD,
∴CG⊥CF,
∴GC是⊙F的切线;
(2)解:①∵CF∥AD,
∴△BCF∽△BDA,
∴![]() =
=![]() ,△BCF的面积:△BDA的面积=1:4,
,△BCF的面积:△BDA的面积=1:4,
∴△BDA的面积=4△BCF的面积=4×15=60;
故答案为:60;
②当∠GCD的度数为30°时,四边形EFCD是菱形.理由如下:
∵CG⊥CF,∠GCD=30°,
∴∠FCB=60°,
∵FB=FC,
∴△BCF是等边三角形,
∴∠B=60°,CF=BF=![]() AB,
AB,
∵AB=AD,
∴△ABD是等边三角形,CF=![]() AD,
AD,
∴∠A=60°,
∵AF=EF,
∴△AEF是等边三角形,
∴AE=AF=![]() AB=
AB=![]() AD,
AD,
∴CF=DE,
又∵CF∥AD,
∴四边形EFCD是平行四边形,
∵CF=EF,
∴四边形EFCD是菱形;
故答案为:30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 等腰三角形底边上的中线就是底边的垂直平分线
B. 等腰三角形的对称轴是底边上的高
C. 一条线段可看做是以它的垂直平分线为对称轴的轴对称图形
D. 等腰三角形的对称轴就是顶角平分线
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a8÷a4=a2
B.(2a2)3=6a6
C.3a3﹣2a2=a
D.3a(1﹣a)=3a﹣3a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】探索与计算:
在△ABC中,BE⊥AC于点E,CD⊥AB于点D,连接DE.
(1)如图1,若∠A=45°,AB=AC,BC=4,求DE的长.
(2)如图2,若∠A=60°,AB与AC不相等,BC=4,求DE的长.
猜想与证明:
(3)根据(1)(2)所求出的结果,猜想DE、BC以及∠A之间的数量关系,并证明.
拓展与应用:
(4)如图3,在△ABC中,AB=BC=5,AC=2
 ,BE⊥AC于点E,CD⊥AB于点D,AF⊥BC于点F,求△DEF的周长.
,BE⊥AC于点E,CD⊥AB于点D,AF⊥BC于点F,求△DEF的周长.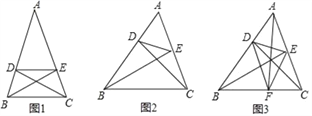
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路部门消息:2017年“端午节”小长假期间,全国铁路客流量达到4640万人次.4640万用科学记数法表示为( )
A.4.64×105
B.4.64×106
C.4.64×107
D.4.64×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(x2﹣mx+1)(x﹣2)的积中不含x2项,则m的值是( )
A.﹣2
B.﹣1
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的坐标系中,画出函数y=2与y=2x+6的图象,并结合图象求:
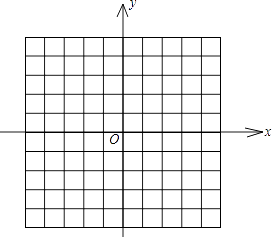
(1)方程2x+6=0的解;
(2)不等式2x+6>2的解集.
相关试题

