【题目】探索与计算:
在△ABC中,BE⊥AC于点E,CD⊥AB于点D,连接DE.
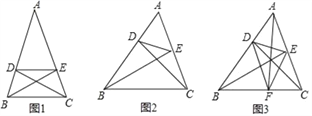
(1)如图1,若∠A=45°,AB=AC,BC=4,求DE的长.
(2)如图2,若∠A=60°,AB与AC不相等,BC=4,求DE的长.
猜想与证明:
(3)根据(1)(2)所求出的结果,猜想DE、BC以及∠A之间的数量关系,并证明.
拓展与应用:
(4)如图3,在△ABC中,AB=BC=5,AC=2![]() ,BE⊥AC于点E,CD⊥AB于点D,AF⊥BC于点F,求△DEF的周长.
,BE⊥AC于点E,CD⊥AB于点D,AF⊥BC于点F,求△DEF的周长.
参考答案:
【答案】(1) DE=2![]() ;(2) DE =2;(3) DE=BCcosA,证明见解析;(4) △DEF的周长=
;(2) DE =2;(3) DE=BCcosA,证明见解析;(4) △DEF的周长=![]() .
.
【解析】试题分析:(1)根据等腰直角三角形的性质得到AE=BE=![]() AB,根据相似三角形的判定定理得到△ADE∽△ABC,根据相似三角形的性质计算;
AB,根据相似三角形的判定定理得到△ADE∽△ABC,根据相似三角形的性质计算;
(2)根据直角三角形的性质得到AE=![]() AB,AD=
AB,AD=![]() AC,根据相似三角形的判定定理得到△ADE∽△ACB,根据相似三角形的性质计算;
AC,根据相似三角形的判定定理得到△ADE∽△ACB,根据相似三角形的性质计算;
(3)根据余弦的概念、相似三角形的判定和性质解答;
(4)根据(3)的结论、三角形的面积公式、勾股定理计算即可.
试题解析:
(1)∵BE⊥AC,∠A=45°,
∴AE=BE=![]() AB,
AB,
同理,AD=CD=![]() AC,
AC,
∵AB=AC,
∴AE=AD,
∴![]() =
=![]() ,又∠A=∠A,
,又∠A=∠A,
∴△ADE∽△ABC,
∴![]() =
=![]() =
=![]() ,
,
∴DE=2![]() ;
;
(2)∵BE⊥AC,∠A=60°,
∴AE=![]() AB,
AB,
同理,AD=![]() AC,
AC,
∴![]() =
=![]() ,又∠A=∠A,
,又∠A=∠A,
∴△ADE∽△ACB,
∴![]() =
=![]() ,
,
∴DE=![]() BC=2;
BC=2;
(3)猜想:DE=BCcosA.
证明:∵BE⊥AC,
∴cosA=![]() ,
,
∴AE=ABcosA,
同理,AD=ACcosA,
∴∴△ADE∽△ACB,
∴![]() =cosA,
=cosA,
∴DE=BCcosA;
(4)∵AB=BC=5,AC=2![]() ,BE⊥AC,
,BE⊥AC,
∴AE=EC=![]() ,
,
由勾股定理得,BE=![]() =2
=2![]() ,
,
∵BC×AF=AC×BE,
∴AF=4,
由勾股定理得,BF=3,
∴cos∠ABC=![]() =
=![]() ,cos∠ACB=cos∠BAC=
,cos∠ACB=cos∠BAC=![]() ,
,
∴EF=DE=ABcos∠ACB=![]() ,DF=ACcos∠ABC=
,DF=ACcos∠ABC=![]() ,
,
∴△DEF的周长=DE+EF+DF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 等腰三角形底边上的中线就是底边的垂直平分线
B. 等腰三角形的对称轴是底边上的高
C. 一条线段可看做是以它的垂直平分线为对称轴的轴对称图形
D. 等腰三角形的对称轴就是顶角平分线
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a8÷a4=a2
B.(2a2)3=6a6
C.3a3﹣2a2=a
D.3a(1﹣a)=3a﹣3a2 -
科目: 来源: 题型:
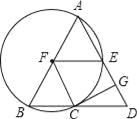
查看答案和解析>>【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路部门消息:2017年“端午节”小长假期间,全国铁路客流量达到4640万人次.4640万用科学记数法表示为( )
A.4.64×105
B.4.64×106
C.4.64×107
D.4.64×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(x2﹣mx+1)(x﹣2)的积中不含x2项,则m的值是( )
A.﹣2
B.﹣1
C.1
D.2
相关试题

