【题目】如图,A(2,0),D(6,4),将线段AD平移得到BC,B(0,﹣6),延长BC交x轴于点E.
(1)则△ABC的面积是 ;
(2)Q为x轴上一动点,当△ABC与△ADQ的面积相等时,试求点Q的坐标.
(3)若存在一点M(m,6)且△ADM的面积不小于△ABC的面积,求m的取值范围.

参考答案:
【答案】(1)△ABC的面积为8;(2)当△ABC与△ADQ的面积相等时,点Q的坐标为(﹣2,0)或(6,0);(3)△ADM的面积不小于△ABC的面积,m的取值范围为m≤4或m≥12.
【解析】
(1)连接AC作CH⊥AE于H,根据平移的性质求出点C的坐标,根据梯形的面积公式、三角形的面积公式计算即可;
(2)设点Q的坐标为(x,0),根据题意列出方程,解方程即可;
(3)直线BC的解析式为y=x-6,直线y=x-6交直线y=6于M′(12,6),此时△ADM′的面积=8,由A(2,0),D(6,4),推出直线AD的解析式为y=x-2,直线y=x-2交y轴于P(0,-2),在y轴上取一点N,使得PN=PB,则N(0,2),作NM∥AD,直线MN的解析式为y=x+2,直线MN交直线y=6于M(4,6),此时△ADM的面积=8,由此几何图形即可解决问题.
(1)如图1中,连接AC作CH⊥AE于H,

∵点A的坐标为(2,0),点B的坐标为(0,﹣6),
∴点A先向左移动2个单位,再向下移动6个单位得到点B,
∵点D的坐标为(6,4),
∴点C的坐标为(4,﹣2),
∴△ABC的面积=![]() ×(2+6)×4﹣
×(2+6)×4﹣![]() ×2×6﹣
×2×6﹣![]() ×2×2=8,
×2×2=8,
故答案为:8;
(2)设点Q的坐标为(x,0)
由题意得,![]() ×|x﹣2|×4=8,
×|x﹣2|×4=8,
解得,x=﹣2或6,
∴当△ABC与△ADQ的面积相等时,点Q的坐标为(﹣2,0)或(6,0);
(3)如图2中,
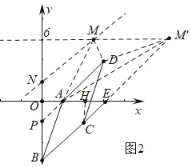
∵B(0,﹣6),C(4,﹣2),
∴直线BC的解析式为y=x﹣6,直线y=x﹣6交直线y=6于M′(12,6),此时△ADM′的面积=8,
∵A(2,0),D(6,4),
∴直线AD的解析式为y=x﹣2,直线y=x﹣2交y轴于P(0,﹣2),
在y轴上取一点N,使得PN=PB,则N(0,2),作NM∥AD,
直线MN的解析式为y=x+2,直线MN交直线y=6于M(4,6),此时△ADM的面积=8,
∴△ADM的面积不小于△ABC的面积,m的取值范围为m≤4或m≥12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
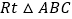 中,
中,  ,AB=BC,A,B的坐标分别为
,AB=BC,A,B的坐标分别为  ,将
,将  绕点P旋转
绕点P旋转  后得到
后得到  ,其中点B的对应点
,其中点B的对应点  的坐标为
的坐标为  .
.
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:

(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类且定价为15元的图书.书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠,学校如果多买12本,则可以享受优惠且所花钱数与原来相同,问学校获奖的同学有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某小区要用篱笆围成一矩形花坛,花坛的一边用足够长的墙,另外三边所用的篱笆之和恰好为
 米.
米.
(1)求矩形 的面积(用
的面积(用  表示,单位:平方米)与边
表示,单位:平方米)与边  (用
(用  表示,单位:米)之间的函数关系式(不要求写出自变量
表示,单位:米)之间的函数关系式(不要求写出自变量  的取值范围);怎样围,可使花坛面积最大?
的取值范围);怎样围,可使花坛面积最大?
(2)如何围,可使此矩形花坛面积是 平方米?
平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
相关试题

