【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.

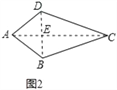
(l)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探宄:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证)
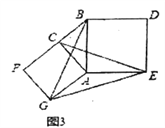
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
参考答案:
【答案】(1)四边形ABCD是垂美四边形,理由见解析;(2)猜想结论:垂美四边形的两组对边的平方和相等,过程见解析;(3)GE=![]()
【解析】试题分析:(1)根据垂直平分线的判定定理可得,直线AC是线段BD的垂直平分线,结论得证;
(2)根据垂直的定义可得∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得AD2+BC2=AE2+DE2+BE2+CE2,进而得到答案;
(3)连接CG、BE,由题意易得△GAB≌△CAE,可知∠ABG=∠AEC,进而得到四边形BCGE是垂美四边形;接下来根据垂美四边形的性质、勾股定理以及(2)的结论进行计算求解,即可完成解答.
试题解析:
解:(1)四边形ABCD是垂美四边形.
证明:∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:垂美四边形的两组对边的平方和相等.
如图2,已知四边形ABCD中,AC⊥BD,垂足为E,
求证:AD2+BC2=AB2+CD2
证明:∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2;
(3)连接CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
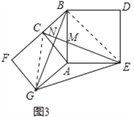
在△GAB和△CAE中,
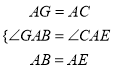 ,
,
∴△GAB≌△CAE,
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4![]() ,BE=5
,BE=5![]() ,
,
∴GE2=CG2+BE2﹣CB2=73,
∴GE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=
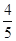 ,反比例函数y=
,反比例函数y= 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.(1)求反比例函数解析式;
(2)若函数y=3x与y=
 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.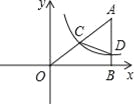
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
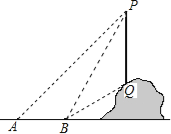
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:
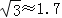 ,
,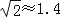 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x∈Z|(x+1)(x﹣4)=0},B={x|x≤a},若A∩B=A,则a的值可以是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(1﹣x)9=a0+a1x+a2x2+…+a9x9 , 则|a1|+|a2|+|a3|+…+|a9|=( )
A.1
B.513
C.512
D.511 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:3ab﹣(3a2﹣3a2b)+3(a2﹣a2b﹣2),其中a=﹣1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 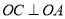 ,
, 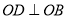 .
.(
 )根据所给的条件用量角器和三角板画出图形.
)根据所给的条件用量角器和三角板画出图形.(
 )求
)求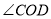 的度数.
的度数.(注意:可能存在不同的情形)
相关试题

