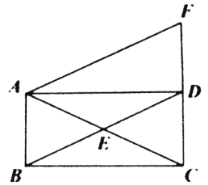
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 中点,延长
中点,延长![]() 到点
到点![]() ,使
,使![]() .
.
(1)求证:![]() ;
;
(2)求证:四边形![]() 为平行四边形;
为平行四边形;
(3)若![]() ,
,![]() ,
,![]() ,直接写出四边形
,直接写出四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)由AAS证明△ADE≌△CBE,即可得出AE=CE;
(2)先证明四边形ABCD是平行四边形,得出AB∥CD,AB=CD,证出AB=DF,即可得出四边形ABDF为平行四边形;
(3)由平行四边形的性质得出∠F=∠DBA,BD=AF=2,AB=DF,证出∠DBA=∠BAC,得出AE=BE=DE,证出∠BAD=90°,由勾股定理求出AD=![]() =
=![]() ,
,
即可得出四边形ABDF的面积.
解答:(1)证明:∵AD∥CB,
∴∠DAC=∠BCA,
∵E为BD中点,
∴DE=BE,
在△ADE和△CBE中,
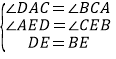
∴△ADE≌△CBE(AAS),
∴AE=CE;
(2)证明:由(1)得:AE=CE,BE=DE,
∴四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵DF=CD,
∴AB∥DF,AB=DF,
∴四边形ABDF为平行四边形;
(3)解:∵四边形ABDF为平行四边形,
∴∠F=∠DBA,BD=AF=2,AB=DF,
∵∠BEC=2∠F,∠BEC=∠DBA+∠BAC,
∴∠DBA=∠BAC,
∴AE=BE=DE,
∴∠BAD=90°,
∵AB=CD=1,
∴AD=![]() =
=![]() ,
,
∵DF=AB=1,
∴四边形ABDF的面积=DF×AD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=
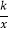 (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.(1)k的值是______;
(2)当t=4时,求△BMN面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是
是 的中点,
的中点, 是边
是边 上一动点,连结
上一动点,连结 ,取
,取 的中点
的中点 ,连结
,连结 .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对 的面积与
的面积与 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:
(1)设
 的长度为
的长度为 ,
, 的面积
的面积 ,通过取
,通过取 边上的不同位置的点
边上的不同位置的点 ,经分析和计算,得到了
,经分析和计算,得到了 与
与 的几组值,如下表:
的几组值,如下表:
0
1
2
3
4
5
6

3

1
0

2
3
根据上表可知,
 ______,
______, ______.
______.(2)在平面直角坐标系
 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.
(3)在(1)的条件下,令
 的面积为
的面积为 .
.①用
 的代数式表示
的代数式表示 .
.②结合函数图象.解决问题:当
 时,
时, 的取值范围为______.
的取值范围为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】宁波至绍兴城际列车已于2019年7月10日运营,这是国内首条利用既有铁路改造开行的跨市域城际铁路.其中余姚至绍兴的成人票价12元/人,学生票价6元/人.余姚某校801班师生共计50人坐城际列车去绍兴秋游.
(1)设有
 名老师,求801班师生从余姚到绍兴的城际列车总费用
名老师,求801班师生从余姚到绍兴的城际列车总费用 关于
关于 的函数表达式.
的函数表达式.(2)若从余姚到绍兴的城际列车总费用
 不超过330元,问至少有几名学生?
不超过330元,问至少有几名学生? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,长方形
 的三个顶点的坐标为
的三个顶点的坐标为 ,
, ,
, ,且
,且 轴,点
轴,点 是长方形内一点(不含边界).
是长方形内一点(不含边界).
(1)求
 ,
, 的取值范围.
的取值范围.(2)若将点
 向左移动8个单位,再向上移动2个单位到点
向左移动8个单位,再向上移动2个单位到点 ,若点
,若点 恰好与点
恰好与点 关于
关于 轴对称,求
轴对称,求 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD=
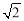 时,求线段BG的长.
时,求线段BG的长.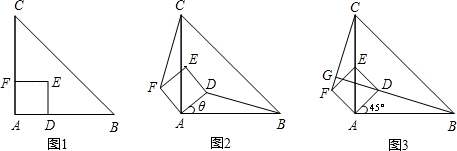
-
科目: 来源: 题型:
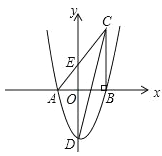
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=
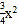 +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
相关试题

