【题目】我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方。即如果一个直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么
,那么![]() 。
。
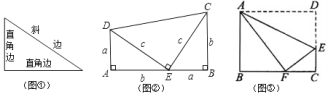
(1)直接填空:如图①,若a=3,b=4,则c= ;若![]() ,
,![]() ,则直角三角形的面积是 ______ 。
,则直角三角形的面积是 ______ 。
(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明![]() 。
。
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?
参考答案:
【答案】(1)5、![]() ;(2)见解析;(3)5
;(2)见解析;(3)5
【解析】
(1)根据勾股定理和三角形面积公式计算即可;
(2)分别用不同的方式表示出梯形的面积,列出等式,根据整式的运算法则计算即可;
(3)根据勾股定理计算.
(1)由勾股定理得,![]() ;
;
∵![]()
∴![]()
∵![]() =9
=9
∴![]() ,解得
,解得![]()
直角三角形面积=![]()
故填:5、![]() ;
;
(2)图②的面积![]()
又图②的面积![]()
∴![]()
∴![]() ,即
,即![]() ;
;
(3)由题意,知AF=AD=10,BC=AD=10,CD=AB=8,
在直角△ABF中,![]() ,即
,即![]() ,
,
∴BF=6
又∵BC=10
∴CF=BCBF=106=4
设EF=x,则DE=x,
∴EC=DCDE=8x,
在直角△ECF中,![]() ,
,
即![]()
解得 x=5,即EF=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=mx+n与反比例函数交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
(1) 若m=k,n=0,求A,B两点的坐标(用m表示).
(2) 如图1,若A(x1,y1)、B(x2,y2),写出y1+y2与n的大小关系,并证明.
(3) 如图2,M、N分别为反比例函数
 图象上的点,AM∥BN∥x轴.若
图象上的点,AM∥BN∥x轴.若 ,且AM,BN之间的距离为5,则k-b=_____________
,且AM,BN之间的距离为5,则k-b=_____________
-
科目: 来源: 题型:
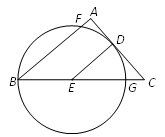
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.

(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组条件中,不能说明
 的是( )
的是( )A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
-
科目: 来源: 题型:
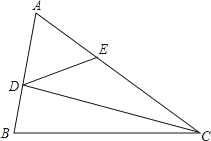
查看答案和解析>>【题目】在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于_____.
-
科目: 来源: 题型:
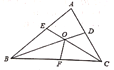
查看答案和解析>>【题目】在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于F,有下列结论:①∠BOE=60°,②∠ABD=∠ACE,③OE=OD,④BC=BE+CD。其中正确的是_________。(把所有正确结论的序号都选上)
相关试题

