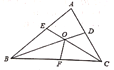
【题目】在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于F,有下列结论:①∠BOE=60°,②∠ABD=∠ACE,③OE=OD,④BC=BE+CD。其中正确的是_________。(把所有正确结论的序号都选上)
参考答案:
【答案】①③④
【解析】
①正确.根据外角的性质得:∠BOE=∠OBC+∠OCB=60°;
②不正确.∠ABD=![]() ∠ABC,∠ACE=
∠ABC,∠ACE=![]() ∠ACB,当AB=AC时,∠ABC=∠ACB,才有∠ABD=∠ACE;
∠ACB,当AB=AC时,∠ABC=∠ACB,才有∠ABD=∠ACE;
③只要证明△BOE≌△BOF,△CDO≌△CFO,即可解决问题;
④根据③中的三角形全等,可得对应边相等,相加可得结论.
解:①如图,∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠OBC+∠OCB=![]() ×120°=60°,
×120°=60°,
∴∠BOE=∠OBC+∠OCB=60°
故①正确;
②∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠ABD=![]() ∠ABC,∠ACE=
∠ABC,∠ACE=![]() ∠ACB,
∠ACB,
当AB=AC时,∠ABC=∠ACB,
而已知AB和AC没有相等关系,
故②不正确;
③∵∠OBC+∠OCB=60°,
∴∠BOC=120°,
∵OF平分∠BOC,
∴∠BOF=∠COF=60°,
∴∠BOE=60°,
∴∠BOE=∠BOF,
在△BOE和△BOF中,
∵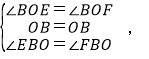
∴△BOE≌△BOF(ASA),
∴OE=OF,
同理得:△CDO≌△CFO,
∴OD=OF,
∴OD=OE,
故③正确;
④∵△BOE≌△BOF,△CDO≌△CFO,
∴BF=BE,CF=CD,
∴BC=CF+BF=BE+CD,
故④正确;
则下列说法中正确的是:①③④
故答案为①③④.
-
科目: 来源: 题型:
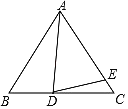
查看答案和解析>>【题目】如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用完全平方公式因式分解在数学中的应用,请回答下列问题:
(1)因式分解:
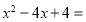 ________.
________.(2)填空:
①当
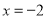 时,代数式
时,代数式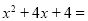 ________;
________;②当
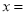 ________时,代数式
________时,代数式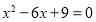 ;
;③代数式
 的最小值是________.
的最小值是________.(3)拓展与应用:求代数式
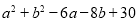 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学期即将结束,为了表彰优秀,班主任王老师用W元钱购买奖品.若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品.设钢笔单价为x元/支,笔记本单价为y元/本.
(1)请用y的代数式表示x.
(2)若用这W元钱全部购买笔记本,总共可以买几本?
(3)若王老师用这W元钱恰好能买30份同样的奖品,可以选择a支钢笔和b本笔记本作为一份奖品(两种奖品都要有).请求出所有可能的a,b值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三名快递员某天的工作情况如图所示,其中点
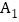 ,
,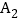 ,
,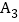 的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点
的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点 ,
, ,
, ,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )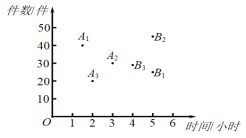
A. ①②B. ①③C. ②D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2+3x-4=0; (2)(x+1)2=4x;
(3)x(x+4)=-5(x+4); (4)2x2-4x-1=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于 x 的方程 2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及 k 值.
相关试题

