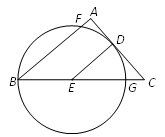
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .
参考答案:
【答案】(1)证明见解析;(2)①⊙E的半径为20;②IE=![]()
【解析】试题分析:(1)证明△CDE∽△CAB,得∠EDC=∠A=90°,所以AC是⊙E的切线;
(2)①如图1,作辅助线,构建矩形AHED,设⊙E的半径为r,表示BH和EC的长,证明△BHE∽△EDC,
列比例式代入r可得结论;
②如图2,作辅助线,构建直角△IME,分别求IM和ME的值,利用勾股定理可求IE的长.
试题解析:(1)∵CDBC=ACCE,
∴![]() ,
,
∵∠DCE=∠ACB,
∴△CDE∽△CAB,
∴∠EDC=∠A=90°,
∴ED⊥AC,
∵点D在⊙E上,
∴AC是⊙E的切线;
(2)①如图1,过E作EH⊥AB于H,
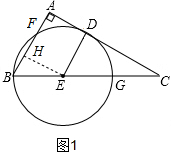
∴BH=FH,
∵∠A=∠AHE=∠ADE=90°,
∴四边形AHED是矩形,
∴ED=AH,ED∥AB,
∴∠B=∠DEC,
设⊙E的半径为r,则EB=ED=EG=r,
∴BH=FH=AH-AF=DE-AF=r-4,
EC=EG+CG=r+5,
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC=90°,
∴△BHE∽△EDC,
∴![]() ,即
,即![]() ,
,
∴r=20,
∴⊙E的半径为20;
②如图2,过I作IM⊥BC于M,过I作IH⊥AB于H,
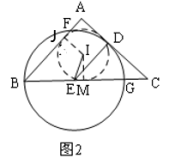
由①得:FH=BH=r-4=20-4=16,AB=AF+2BH=4+2×16=36,
BC=2r+5=2×20+5=45,
∴AC=![]() =27,
=27,
∵I是Rt△ABC的内心,
∴IM=![]() =9,
=9,
∴AH=IM=9,
∴BH=BM=36-9=27,
∴EM=27-20=7,
在Rt△IME中,由勾股定理得:IE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1) 3x-2(x-1)= 2- 3(5-2x)
(2)
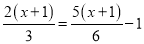
(3)
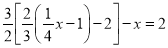
(4)
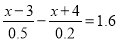
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_________;
(2)仔细观察,在图2中“8字形”的个数_________个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角,其他条件不变,试问∠P与∠D,∠B之间存在着怎样的数量关系(直接写出结论即可)
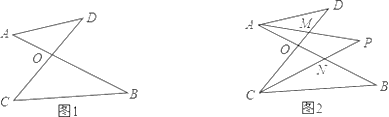
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数 1 至 2024 按一定规律排列成如图所示的 8 列,规定从上到下依次为第 1 行,第 2 行,第 3 行,…从左往右依次为第 1 列至第 8 列.
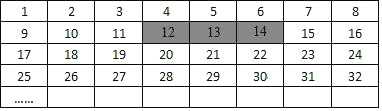
(1)数 56 在第 行 列 ;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为 x,则被框的三个数的和能否等于 2019?若能,请求出 x;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定,若关于 x 的一元一次方程 ax=b 的解为 x=ba,则称该方程的为差解方程,例如:3x=
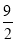 的解为x=
的解为x= 且
且 =
=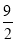 -3,则该方程3x=
-3,则该方程3x=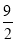 就是差解方程.
就是差解方程.请根据以上规定解答下列问题
(1)若关于 x 的一元一次方程-5x=m+1 是差解方程,则 m=_____.
(2)若关于 x 的一元一次方程 2x=ab+3a+1 是差解方程,且它的解为 x=a,求代数式(ab+2)2019的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
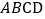 的边长为
的边长为 ,点
,点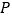 是
是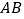 边上的一个动点,连接
边上的一个动点,连接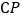 ,过点
,过点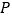 作
作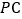 的垂线交
的垂线交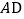 于点
于点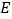 ,以
,以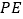 为边作正方形
为边作正方形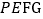 ,顶点
,顶点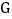 在线段
在线段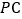 上,对角线
上,对角线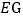 、
、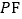 相交于点
相交于点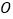 .(1)若
.(1)若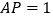 ,则
,则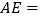 ;
;(2)①求证:点
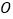 一定在
一定在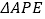 的外接圆上;
的外接圆上;②当点
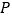 从点
从点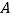 运动到点
运动到点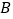 时,点
时,点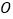 也随之运动,求点
也随之运动,求点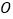 经过的路径长;
经过的路径长;(3)在点
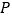 从点
从点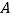 到点
到点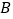 的运动过程中,
的运动过程中,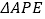 的外接圆的圆心也随之运动,求该圆心到
的外接圆的圆心也随之运动,求该圆心到 边的距离的最大值.
边的距离的最大值.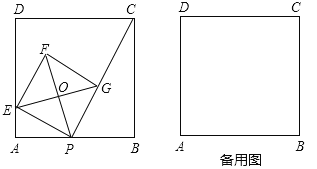
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 是定长线段
是定长线段 上一定点.点
上一定点.点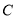 在线段
在线段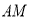 上,点
上,点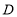 在线段
在线段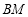 上,
上,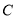 、
、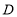 两点分别从
两点分别从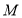 、
、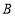 出发,分别以
出发,分别以 /
/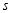 、
、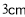 /
/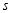 的速度沿直线
的速度沿直线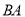 同时向左运动.
同时向左运动.(1)若
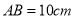 ,当点
,当点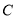 、
、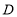 运动了
运动了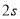 ,求
,求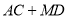 的值;
的值;(2)若点
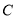 、
、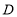 运动时,总有
运动时,总有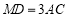 ,则
,则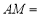 _____
_____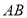 ;
;(3)在(2)的条件下,点
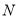 是直线
是直线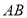 上一点,且
上一点,且 ,求
,求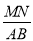 的值.
的值.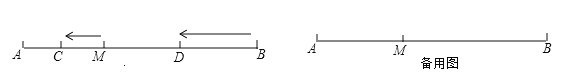
相关试题

