【题目】如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( ) 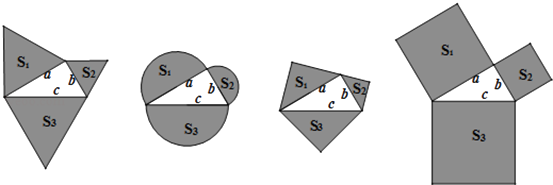
A.1
B.2
C.3
D.4
参考答案:
【答案】D
【解析】解:(1)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 , ∵a2+b2=c2 ,
c2 , ∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 .
(2.)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 .
(3.)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 .
(4.)S1=a2 , S2=b2 , S3=c2 ,
∵a2+b2=c2 ,
∴S1+S2=S3 .
综上,可得
面积关系满足S1+S2=S3图形有4个.
故选:D.
根据直角三角形a、b、c为边,应用勾股定理,可得a2+b2=c2 . (1)第一个图形中,首先根据等边三角形的面积的求法,表示出3个三角形的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 . (2)第二个图形中,首先根据圆的面积的求法,表示出3个半圆的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 . (3)第三个图形中,首先根据等腰直角三角形的面积的求法,表示出3个等腰直角三角形的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 . (4)第四个图形中,首先根据正方形的面积的求法,表示出3个正方形的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取120名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为
 小时);
小时);(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=x2+4先向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
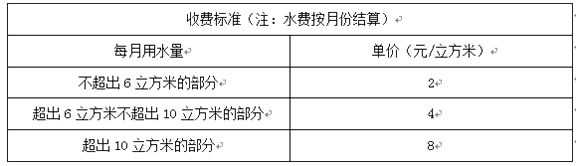
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费元;
(2)若某户居民3月份交水费36元,则用水量为立方米;
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费元.
(4)若某户居民 5、6 两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该居民5、6两个月共交水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为
 ;④
;④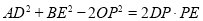 ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .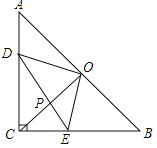
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2)100+(﹣2)99=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包
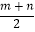 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )
A.盈利了
B.亏损了
C.不赢不亏
D.盈亏不能确定
相关试题

