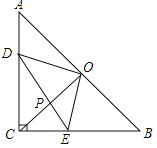
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为![]() ;④
;④![]() ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
参考答案:
【答案】①②③④.
【解析】
试题分析:①正确.如图,∵∠ACB=90°,AC=BC,CO⊥AB
∴AO=OB=OC,∠A=∠B=∠ACO=∠BCO=45°,在△ADO和△CEO中,∵OA=OC,∠A=∠ECO,AD=CE,∴△ADO≌△CEO,∴DO=OE,∠AOD=∠COE,∴∠AOC=∠DOE=90°,∴△DOE是等腰直角三角形.故①正确.
②正确.∵∠DCE+∠DOE=180°,∴D、C、E、O四点共圆,∴∠CDE=∠COE,故②正确.
③正确.∵AC=BC=1,∴S△ABC=![]() ×1×1=
×1×1=![]() ,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=
,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=![]() S△ABC=
S△ABC=![]() ,故③正确.
,故③正确.
④正确.∵D、C、E、O四点共圆,∴OPPC=DPPE,∴![]() +2DPPE=
+2DPPE=![]() +2OPPC=2OP(OP+PC)=2OPOC,∵∠OEP=∠DCO=∠OCE=45°,∠POE=∠COE,∴△OPE∽△OEC,∴
+2OPPC=2OP(OP+PC)=2OPOC,∵∠OEP=∠DCO=∠OCE=45°,∠POE=∠COE,∴△OPE∽△OEC,∴![]() ,∴OPOC=
,∴OPOC=![]() ,∴
,∴![]() +2DPPE=
+2DPPE=![]() =
=![]() =
=![]() ,∵CD=BE,CE=AD,∴
,∵CD=BE,CE=AD,∴![]() ,∴
,∴![]() .
.
故④正确.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=x2+4先向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
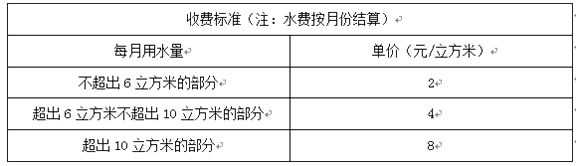
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费元;
(2)若某户居民3月份交水费36元,则用水量为立方米;
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费元.
(4)若某户居民 5、6 两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该居民5、6两个月共交水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )
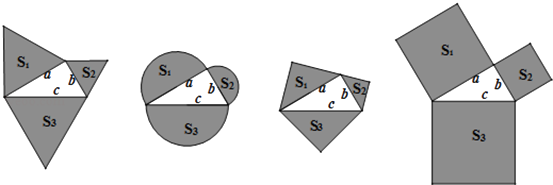
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2)100+(﹣2)99=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包
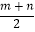 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )
A.盈利了
B.亏损了
C.不赢不亏
D.盈亏不能确定 -
科目: 来源: 题型:
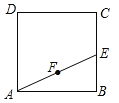
查看答案和解析>>【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
相关试题

