【题目】如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.

(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
参考答案:
【答案】(1)D(1,0);(2)![]() ;(3)
;(3)![]() ;(4)P(6,3).
;(4)P(6,3).
【解析】试题分析:(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)联立方程组,求出交点C的坐标,继而可求出S△ADC;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到AD的距离.
解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,![]() ,代入表达式y=kx+b,
,代入表达式y=kx+b,
∴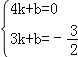 ,
,
∴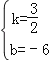 ,
,
∴直线l2的解析表达式为![]() ;
;
(3)由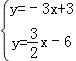 ,
,
解得![]() ,
,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=![]() ×3×|﹣3|=
×3×|﹣3|=![]() ;
;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,直径为
 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0, ).
).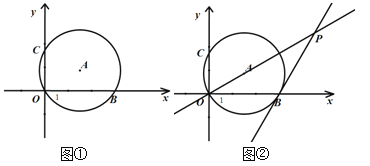
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数
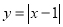 的图象与性质进行了研究,下面是小慧的研究过程,请补充完成:
的图象与性质进行了研究,下面是小慧的研究过程,请补充完成: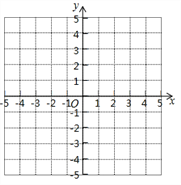
(1)函数
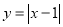 的自变量
的自变量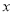 的取值范围是__________;
的取值范围是__________;(2)列表,找出
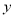 与
与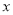 的几组对应值.
的几组对应值.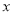
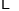
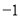
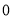
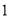
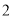
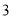
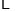
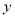
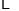
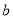
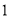
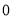
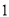
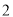
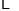
其中,
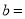 __________;
__________;(3)在平面直角坐标系
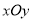 中,描出以上表中各队对应值为坐标的点,并画出该函数的图象;
中,描出以上表中各队对应值为坐标的点,并画出该函数的图象;(4)写出该函数的一条性质:____________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+4的图象经过点(a,8),则a=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值不小于10而小于13的所有整数是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于2且小于5的所有整数的和是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(2,3),B(6,3),连结AB,如果点P在直线y=x-1上 ,且点P到直线AB的距离小于1,那么称点P是线段AB的“邻近点”.

(1)判断点C(
 ,
, )是否是线段AB的“邻近点” ;
)是否是线段AB的“邻近点” ;(2)若点Q(m,n)是线段AB的“邻近点”,则m的取值范围 .
相关试题

