【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)、y=﹣x2+4x;(2)、10;(3)、N1(2+2![]() ,﹣4),N2(2﹣2
,﹣4),N2(2﹣2![]() ,﹣4)
,﹣4)
【解析】试题分析:(1)、根据旋转的性质可求出C的坐标和A的坐标,又因为抛物线经过原点,故设y=ax2+bx把(2,4),(4,0)代入,求出a和b的值即可求出该抛物线的解析式;(2)、四边形PEFM的周长有最大值,设点P的坐标为P(a,﹣a2+4a)则由抛物线的对称性知OE=AF,所以EF=PM=4﹣2a,PE=MF=﹣a2+4a,则矩形PEFM的周长L=2[4﹣2a+(﹣a2+4a)]=﹣2(a﹣1)2+10,利用函数的性质即可求出四边形PEFM的周长的最大值;(3)、在抛物线上存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形,由(1)可求出抛物线的顶点坐标,过点C作x轴的平行线,与x轴没有其它交点,过y=﹣4作x轴的平行线,与抛物线有两个交点,这两个交点为所求的N点坐标所以有﹣x2+4x=﹣4,解方程即可求出交点坐标.
试题解析:(1)、因为OA=4,AB=2,把△AOB绕点O逆时针旋转90°,
可以确定点C的坐标为(2,4);由图可知点A的坐标为(4,0),
又因为抛物线经过原点,故设y=ax2+bx把(2,4),(4,0)代入,得![]() ,解得
,解得![]()
所以抛物线的解析式为y=﹣x2+4x;
(2)、四边形PEFM的周长有最大值,理由如下:
由题意,如图所示,设点P的坐标为P(a,﹣a2+4a)则由抛物线的对称性知OE=AF,
∴EF=PM=4﹣2a,PE=MF=﹣a2+4a,
则矩形PEFM的周长L=2[4﹣2a+(﹣a2+4a)]=﹣2(a﹣1)2+10,
∴当a=1时,矩形PEFM的周长有最大值,Lmax=10;
(3)、在抛物线上存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形,理由如下:
∵y=﹣x2+4x=﹣(x﹣2)2+4可知顶点坐标(2,4),
∴知道C点正好是顶点坐标,知道C点到x轴的距离为4个单位长度,
过点C作x轴的平行线,与x轴没有其它交点,过y=﹣4作x轴的平行线,与抛物线有两个交点,
这两个交点为所求的N点坐标所以有﹣x2+4x=﹣4 解得x1=2+![]() ,x2=2﹣
,x2=2﹣![]()
∴N点坐标为N1(2+![]() ,﹣4),N2(2﹣
,﹣4),N2(2﹣![]() ,﹣4).
,﹣4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①一条直线的平行线只有一条:
②过一点可以作一条直线与已知直线平行;
③过一点作直线的平行线仅有一条或不存在;
④过直线外一点有且只有一条直线与已知直线平行.
A. 1个
B. 2个
C. 3个
D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,书桌上的一种新型台历和一块主板AB、一个架板AC和环扣(不计宽度,记为点A)组成,其侧面示意图为△ABC,测得AC⊥BC,AB=5cm,AC=4cm,现为了书写记事方便,须调整台历的摆放,移动点C至C′,当∠C′=30°时,求移动的距离即CC′的长(或用计算器计算,结果取整数,其中
 =1.732,
=1.732,  =4.583)
=4.583)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.

(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果l1∥l2,l2∥l3,l3∥l4,那么l1与l4的关系是( )
A. 平行
B. 相交
C. 重合
D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课外小组为了解本校2014-2015学年八年级700名学生每学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了如下的频数分布表和频数分布直方图(各组数据包括最小值,不包括最大值).
(1)补全下面的频数分布表和频数分布直方图: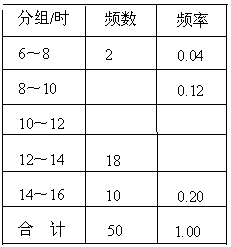

(2)可以估计这所学校2014-2015学年八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人? -
科目: 来源: 题型:
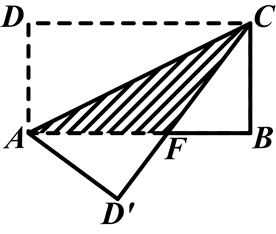
查看答案和解析>>【题目】如图所示,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,使点D落在点D′处,求重叠部分△AFC的面积.
相关试题

