【题目】如图所示,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,使点D落在点D′处,求重叠部分△AFC的面积.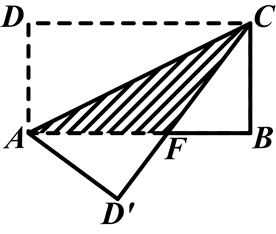
参考答案:
【答案】解:在长方形ABCD中,
∵AB∥CD,
∴∠BAC=∠DCA.
又由折叠的性质可得∠DCA=∠FCA.
∴∠BAC=∠FCA.
∴AF=CF.
设AF=x,则BF=AB-AF=8-x.
在Rt△BCF中,BC=4,BF=8-x,CF=x,
∴42+(8-x)2=x2 . 解得x=5.
∴ ![]() .
.
【解析】由矩形性质得到∠BAC=∠DCA;由折叠的性质得∠DCA=∠FCA;根据等量代换可得∠BAC=∠FCA;由等边对等角得AF=CF.设AF=x,则BF=AB-AF=8-x.在Rt△BCF中,由勾股定理得到一个一元二次方程,42+(8-x)2=x2 . 解得x=5.再由三角形面积公式即可求得。
【考点精析】本题主要考查了三角形的面积和勾股定理的概念的相关知识点,需要掌握三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果l1∥l2,l2∥l3,l3∥l4,那么l1与l4的关系是( )
A. 平行
B. 相交
C. 重合
D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课外小组为了解本校2014-2015学年八年级700名学生每学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了如下的频数分布表和频数分布直方图(各组数据包括最小值,不包括最大值).
(1)补全下面的频数分布表和频数分布直方图: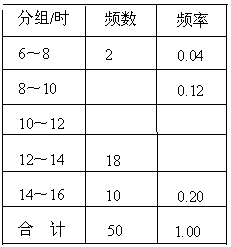

(2)可以估计这所学校2014-2015学年八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2x2-18=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:
(2)(﹣a2)3﹣(﹣a3)2+2a5(﹣a)
(3)(2a+b)(2a-b)+3(2a-b) 2+(-3a)(4a-3b) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.

相关试题

