【题目】某中学七年级一班在一次活动中要分为四个组,其中第一组有x人,第二组比第一组的![]() 少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.
少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.
(1)用含x的代数式表示第二、三、四组的人数,把答案填在下表相应的位置:
第一组 | 第二组 | 第三组 | 第四组 |
x人 |
|
|
|
x=12 |
|
|
|
(2)求x=12时第二、三、四组的人数,把答案填在上表相应的位置;
(3)求七年级一班的总人数(用含x的代数式表示),并求x=10时,该班的总人数;
(4)x能否等于13,为什么?x能否等于6,为什么?
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)39;(4)x不能等于13,x不能等于6.
【解析】
(1)根据题意可用含x的代数式表示第二、三、四组的人数;
(2)把x=12代入计算可求第二、三、四组的人数;
(3)先求七年级一班的总人数(用含x的代数式表示),再把x=10代入可求该班的总人数;
(4)分别把x=13,x=6代入计算,根据整数的性质即可求解.
解:(1)填表如下:
(2)当x=12时,
![]() x﹣5=18﹣5=13,
x﹣5=18﹣5=13,
![]() x﹣20=30﹣20=10,
x﹣20=30﹣20=10,
34﹣2x=34﹣24=10,
填表如下:
第一组 | 第二组 | 第三组 | 第四组 |
x人 |
|
| 34﹣2x |
x=12 | 13 | 10 | 10 |
(3)x+![]() x﹣5+
x﹣5+![]() x﹣20+34﹣2x=3x+9,
x﹣20+34﹣2x=3x+9,
当x=10时,3x+9=30+9=39;
(4)当x=13时,
![]() x﹣5=19.5﹣5=14.5,
x﹣5=19.5﹣5=14.5,
∵14.5不是整数,
∴x不能等于13;
当x=6时,
![]() x﹣20=15﹣20=﹣5,
x﹣20=15﹣20=﹣5,
∵﹣5是负数,
∴x不能等于6.
-
科目: 来源: 题型:
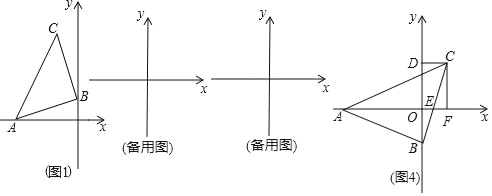
查看答案和解析>>【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有( )
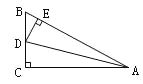
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
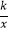 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.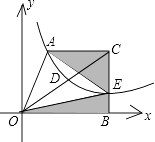
(1)填空:双曲线的另一支在第象限,k的取值范围是;
(2)若点C的坐标为(2,2),当点E在什么位置时,阴影部分的面积S最小?
(3)若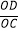 =
=  ,S△OAC=2,求双曲线的解析式.
,S△OAC=2,求双曲线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )
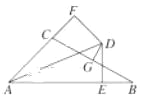
A. 6 B. 3 C. 2 D. 1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2
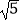 .
. 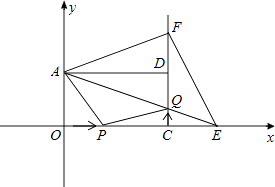
(1)求点D的坐标,并直接写出t的取值范围.
(2)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
(3)在(2)的条件下,t为何值时,四边形APQF是梯形?
相关试题

