【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y= ![]() 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.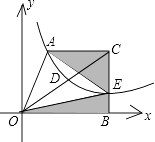
(1)填空:双曲线的另一支在第象限,k的取值范围是;
(2)若点C的坐标为(2,2),当点E在什么位置时,阴影部分的面积S最小?
(3)若 ![]() =
= ![]() ,S△OAC=2,求双曲线的解析式.
,S△OAC=2,求双曲线的解析式.
参考答案:
【答案】
(1)三;k>0
(2)
解:∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,
而点C的坐标为(2,2),
∴A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),
把y=2代入y= ![]() 得x=
得x= ![]() ;把x=2代入y=
;把x=2代入y= ![]() 得y=
得y= ![]() ,
,
∴A点的坐标为( ![]() ,2),E点的坐标为(2,
,2),E点的坐标为(2, ![]() ),
),
∴S阴影部分=S△ACE+S△OBE
= ![]() ×(2﹣
×(2﹣ ![]() )×(2﹣
)×(2﹣ ![]() )+
)+ ![]() ×2×
×2× ![]()
= ![]() k2﹣
k2﹣ ![]() k+2
k+2
= ![]() (k﹣2)2+
(k﹣2)2+ ![]() ,
,
当k﹣2=0,即k=2时,S阴影部分最小,最小值为 ![]() ;
;
∴E点的坐标为(2,1),即E点为BC的中点,
∴当点E在BC的中点时,阴影部分的面积S最小;
(3)
解:设D点坐标为(a, ![]() ),
),
∵ ![]() =
= ![]() ,
,
∴2OD=OC,即D点为OC的中点,
∴C点坐标为(2a, ![]() ),
),
∴A点的纵坐标为 ![]() ,
,
把y= ![]() 代入y=
代入y= ![]() 得x=
得x= ![]() ,
,
∴A点坐标为( ![]() ,
, ![]() ),
),
∵S△OAC=2,
∴ ![]() ×(2a﹣
×(2a﹣ ![]() )×
)× ![]() =2,
=2,
∴k= ![]() ,
,
∴双曲线的解析式为y= ![]() .
.
【解析】(1)根据反比例函数图象与性质得到:双曲线y= ![]() 的一支在第一象限,则k>0,得到另一支在第三象限;(2)根据梯形的性质,AC∥x轴,BC⊥x轴,而点C的坐标为(2,2),则A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),再分别把y=2或x=2代入y=
的一支在第一象限,则k>0,得到另一支在第三象限;(2)根据梯形的性质,AC∥x轴,BC⊥x轴,而点C的坐标为(2,2),则A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),再分别把y=2或x=2代入y= ![]() 可得到A点的坐标为(
可得到A点的坐标为( ![]() ,2),E点的坐标为(2,
,2),E点的坐标为(2, ![]() ),然后计算S阴影部分=S△ACE+S△OBE=
),然后计算S阴影部分=S△ACE+S△OBE= ![]() ×(2﹣
×(2﹣ ![]() )×(2﹣
)×(2﹣ ![]() )+
)+ ![]() ×2×
×2× ![]() =
= ![]() k2﹣
k2﹣ ![]() k+2,配方得
k+2,配方得 ![]() (k﹣2)2+
(k﹣2)2+ ![]() ,当k=2时,S阴影部分最小值为
,当k=2时,S阴影部分最小值为 ![]() ,则E点的坐标为(2,1),即E点为BC的中点;(3)设D点坐标为(a,
,则E点的坐标为(2,1),即E点为BC的中点;(3)设D点坐标为(a, ![]() ),由
),由 ![]() =
= ![]() ,则2OD=OC,即D点为OC的中点,于是C点坐标为(2a,
,则2OD=OC,即D点为OC的中点,于是C点坐标为(2a, ![]() ),得到A点的纵坐标为
),得到A点的纵坐标为 ![]() ,把y=
,把y= ![]() 代入y=
代入y= ![]() 得x=
得x= ![]() ,确定A点坐标为(
,确定A点坐标为( ![]() ,
, ![]() ),根据三角形面积公式由S△OAC=2得到
),根据三角形面积公式由S△OAC=2得到 ![]() ×(2a﹣
×(2a﹣ ![]() )×
)× ![]() =2,然后解方程即可求出k的值.
=2,然后解方程即可求出k的值.
-
科目: 来源: 题型:
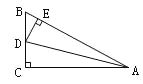
查看答案和解析>>【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
-
科目: 来源: 题型:
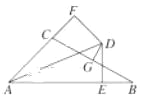
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级一班在一次活动中要分为四个组,其中第一组有x人,第二组比第一组的
 少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.
少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.(1)用含x的代数式表示第二、三、四组的人数,把答案填在下表相应的位置:
第一组
第二组
第三组
第四组
x人
x=12
(2)求x=12时第二、三、四组的人数,把答案填在上表相应的位置;
(3)求七年级一班的总人数(用含x的代数式表示),并求x=10时,该班的总人数;
(4)x能否等于13,为什么?x能否等于6,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )
A. 6 B. 3 C. 2 D. 1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2
 .
. 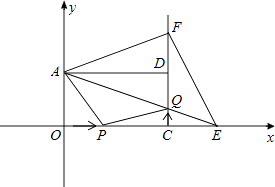
(1)求点D的坐标,并直接写出t的取值范围.
(2)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
(3)在(2)的条件下,t为何值时,四边形APQF是梯形? -
科目: 来源: 题型:
查看答案和解析>>【题目】为提倡全民健身活动, 某社区准备购买羽毛球和羽毛球拍供社区居民使用, 某体育用品商店羽毛球每盒 10 元, 羽毛球拍每副 40 元 .该商店有两种优惠方案,方案一: 不购买会员卡时, 羽毛球享受 8.5 折优惠, 羽毛球拍购买 5 副(含5 副) 以上才能享受 8.5 折优惠, 5 副以下必须按定价购买;方案二: 每张会员卡 20 元, 办理会员卡时, 全部商品享受 8 折优惠 . 设该社区准备购买羽毛球拍 6 副, 羽毛球
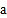 盒, 请回答下列问题:
盒, 请回答下列问题:(1)如果一位体育爱好者按方案一只购买了 4 副羽毛球拍,求他购买时所需要的费用;
(2)用含
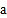 的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
的代数式分别表示该社区按方案一和方案二购买所需要的钱数;(3)①直接写出一个
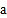 的值, 使方案一比方案二优惠;
的值, 使方案一比方案二优惠;②直接写出一个
 的值, 使方案二比方案一优惠 .
的值, 使方案二比方案一优惠 .
相关试题

