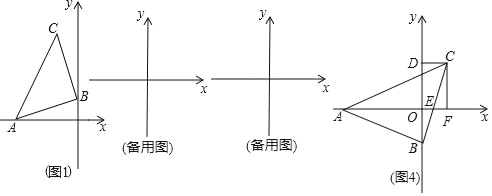
【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
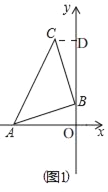
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).
参考答案:
【答案】(1)C(﹣1,4);(2)OD=a﹣b;(3)aAE+bCF=﹣a(a+b).
【解析】
(1)先确定出OA=3,OB=1,进而判断出△AOB≌△BDC,即可得出BD=3,CD=1,即可得出结论;
(2)分三种情况,同(1)的方法即可得出结论;
(3)先确定出OF=CD=﹣b,CF=OD=b﹣a,进而得出AF=OA+OF=﹣a﹣b,在判断出△AOB∽△CFE,即可得出EF=![]() (b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣
(b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),即可得出结论.
(b﹣a),即可得出结论.
解:(1)如图1,
∵点A的坐标为(﹣3,0),点B的坐标为(0,1),
∴OA=3,OB=1,
过点C作CD⊥y轴于D,
∴∠BCD+∠CBD=90°,
∵∠ABC=90°,
∴∠CBD+∠ABO=90°,
∴∠ABO=∠BCD,
在△AOB和△BDC中,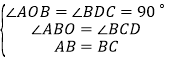 ,
,
∴△AOB≌△BDC,
∴BD=OA=3,CD=OB=1,
∴OD=OB+BD=4,
∴C(﹣1,4);
(2)当点B在y轴正半轴上时,
如图1,∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=b,
∴OD=OB+BD=b+(﹣a)=b﹣a,
当点B在y轴负半轴上,点C在第一象限时,如图2,
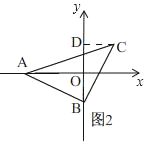
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
当点B在y轴负半轴,点C在第四象限时,如图3,

∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=OB﹣BD=﹣b﹣(﹣a)=a﹣b;
(3)如图4,
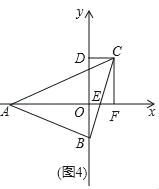
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
∵CF⊥OA于F,
∴四边形ODCF是矩形,
∴OF=CD=﹣b,CF=OD=b﹣a,
∴AF=OA+OF=﹣a﹣b,
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵AF平分∠BAC,
∴∠OAC=∠OAB=22.5°,
∴∠ECF=∠ACF﹣∠ACB=90°﹣∠OAC﹣∠ACB=22.5°=∠OAB,
∵∠AOB=∠CFE,
∴△AOB∽△CFE,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() (b﹣a),
(b﹣a),
∴AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),
(b﹣a),
∵CF=b﹣a,
∴AE=﹣a﹣b﹣![]() CF,
CF,
∴aAE+bCF=﹣a(a+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.

(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)
 .
.【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=
 ,
,∴DP=
 .
.【题型】解答题
【结束】
25【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
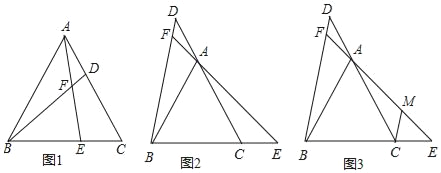
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有( )
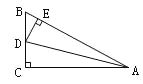
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级一班在一次活动中要分为四个组,其中第一组有x人,第二组比第一组的
 少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.
少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.(1)用含x的代数式表示第二、三、四组的人数,把答案填在下表相应的位置:
第一组
第二组
第三组
第四组
x人
x=12
(2)求x=12时第二、三、四组的人数,把答案填在上表相应的位置;
(3)求七年级一班的总人数(用含x的代数式表示),并求x=10时,该班的总人数;
(4)x能否等于13,为什么?x能否等于6,为什么?
相关试题

