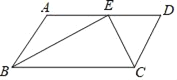
【题目】已知:如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.求ABCD的周长和面积.
参考答案:
【答案】平行四边形的周长为39cm,面积为60cm2.
【解析】试题分析:根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13.根据等腰三角形的性质得到AB=CD=![]() AD=
AD=![]() BC=6.5,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
BC=6.5,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
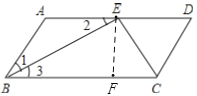
试题解析:∵BE、CE分别平分∠ABC、∠BCD,
∴∠1=∠3=![]() ∠ABC,∠DCE=∠BCE=
∠ABC,∠DCE=∠BCE=![]() ∠BCD,
∠BCD,
∵AD∥BC,AB∥CD,
∴∠2=∠3,∠BCE=∠CED,∠ABC+∠BCD=180°,
∴∠1=∠2,∠DCE=∠CED,∠3+∠BCE=90°,
∴AB=AE,CD=DE,∠BEC=90°,
在直角三角形BCE中,根据勾股定理得:BC=13,
根据平行四边形的对边相等,得到:AB=CD,AD=BC,
∴平行四边形的周长等于:13+13+13=39;
作EF⊥BC于F.根据直角三角形的面积公式得:EF=![]() =
=![]()
所以平行四边形的面积=![]() ×13=60;
×13=60;
即平行四边形的周长为39cm,面积为60cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,若sinA=
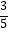 , 则cosB的值是( )
, 则cosB的值是( )
A.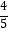
B.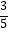
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB,点P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点.
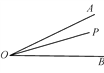
(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长的最小值为4,则∠AOB=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
-
科目: 来源: 题型:
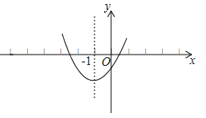
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=﹣1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.
相关试题

