【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=﹣1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.其中正确的结论有( )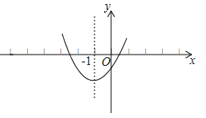
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】B
【解析】解:(1)抛物线与x轴有2个交点,则b2﹣4ac>0,则b2>4ac,故(1)正确;
(2)抛物线开口方向向上,则a>0.
抛物线与y轴交于负半轴,则c<0.
对称轴在y轴的左侧,a、b同号,即b>0.
所以abc<0.故(2)错误;
(3)对称轴x=﹣![]() =﹣1,则b﹣2a=0,故(3)错误;
=﹣1,则b﹣2a=0,故(3)错误;
(4)如图,当x=1时,y>0,即a+b+c>0,故(4)正确;
(5)如图,当x=﹣时,y<0,即a﹣b+c<0.故(5)正确;
综上所述,正确的个数是3个.
故选:B.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

-
科目: 来源: 题型:
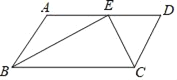
查看答案和解析>>【题目】已知:如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.求ABCD的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角∠A CA′的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】圆的内接等腰三角形ABC,圆的半径为10,如果底边BC的长为16,那么△ABC的面积为
相关试题

