【题目】如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,求⊙O的半径.

参考答案:
【答案】![]()
【解析】试题分析:设AC、AB与⊙O的切点分别为R、M,连接OR、OM,过O作OK⊥BC于K;由于△POR∽△PCB,可得出关于PR,OR,PC,BC的比例关系式,由此可求出PR与半径的比例关系.由此可表示出OK,AP的长;在Rt△OBK中,已知了OK的表达式,BK=BC-r,而OB可在Rt△OBM中用勾股定理求得.由此可根据勾股定理求出半径r的长.
试题解析:
连接OR、OM,如图所示:
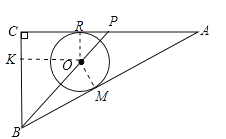
则OR⊥AC,OM⊥AB;过O作OK⊥BC于K,
设⊙O的半径为r,
易知:△POR∽△PBC,
![]() ,
,
∵BC=![]() cm,
cm,
∴![]() ,即PR=
,即PR=![]() ,
,
AP=CP=2×2=4cm,
在Rt△BOK与Rt△BMO中,根据勾股定理,得:
![]() ,
,
解得:r=![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=
 .其中正确的结论是()
.其中正确的结论是()
A.①②③④B.①④C.①②④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.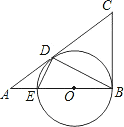
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一台灯示意图,其中灯头连接杆DE始终和桌面FG平行,灯脚AB始终和桌面FG垂直,

(1)当∠EDC=∠DCB=120°时,求∠CBA;
(2)连杆BC、CD可以绕着B、C和D进行旋转,灯头E始终在D左侧,设∠EDC,∠DCB,∠CBA的度数分别为α,β,γ,请画出示意图,并直接写出示意图中α,β,γ之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有除颜色外都相同的6个红球和4个黄球,从袋子中任意摸出一个球,请问:
(1)“摸出的球是白球”是什么事件?
(2)“摸出的球是红球”是什么事件?
(3)“摸出的球不是绿球”是什么事件?
(4)摸出哪种颜色球的可能性最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
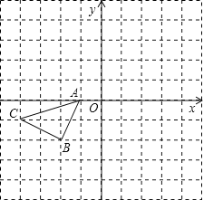
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△AB1C1关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标.
相关试题

