【题目】如图为一台灯示意图,其中灯头连接杆DE始终和桌面FG平行,灯脚AB始终和桌面FG垂直,

(1)当∠EDC=∠DCB=120°时,求∠CBA;
(2)连杆BC、CD可以绕着B、C和D进行旋转,灯头E始终在D左侧,设∠EDC,∠DCB,∠CBA的度数分别为α,β,γ,请画出示意图,并直接写出示意图中α,β,γ之间的数量关系.
参考答案:
【答案】(1)∠CBA=150°,(2)α+β-γ=90°.
【解析】
(1)过C作CP∥DE,延长CB交FG于H,依据平行线的性质,即可得到∠CHA=∠PCH=60°,依据三角形外角性质,即可得到∠CBA的度数;
(2)过C作CP∥DE,延长CB交FG于H,依据平行线的性质,即可得到∠D+∠DCH+∠FHC=360°,再根据三角形外角性质,即可得到α,β,γ之间的数量关系.
(1)如图,过C作CP∥DE,延长CB交FG于H,
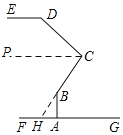
∵DE∥FG,
∴PC∥FG,
∴∠PCD=180°-∠D=60°,∠PCH=120°-∠PCD=60°,
∴∠CHA=∠PCH=60°,
又∵∠CBA是△ABH的外角,AB⊥FG,
∴∠CBA=60°+90°=150°,
(2)如图,延长CB交FG于H,
∵DE∥FG,
∴PC∥FG,
∴∠D+∠PCD=180°,∠FHC+∠PCH=180°,
∴∠D+∠DCH+∠FHC=360°,
又∵∠CBA是△ABH的外角,AB⊥FG,
∴∠AHB=∠ABC-90°,
∴∠FHC=180°-(∠ABC-90°)=270°-∠ABC,
∴∠D+∠DCH+270°-∠ABC=360°,即∠D+∠DCB-∠ABC=90°.
即α+β-γ=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长:中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表

组别
海选成绩x
A组
50≤x<60
B组
60≤x<70
C组
70≤x<80
D组
80≤x<90
E组
90≤x<100
请根据所给信息,解答下列问题
①图1条形统计图中D组人数有多少?
②在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角的度数为 度;
③规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=
 .其中正确的结论是()
.其中正确的结论是()
A.①②③④B.①④C.①②④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.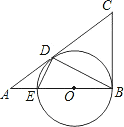
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有除颜色外都相同的6个红球和4个黄球,从袋子中任意摸出一个球,请问:
(1)“摸出的球是白球”是什么事件?
(2)“摸出的球是红球”是什么事件?
(3)“摸出的球不是绿球”是什么事件?
(4)摸出哪种颜色球的可能性最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
相关试题

