【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=![]() .其中正确的结论是()
.其中正确的结论是()

A.①②③④B.①④C.①②④D.①③④
参考答案:
【答案】D
【解析】
①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明即可判断出①正确;
②根据菱形的对角线平分一组对角可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,即可判断出②错误;
③点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,即可判断出③正确;
④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,即可判断出④正确.
①∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,故①正确;
②∵四边形CFHE是菱形,
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,故②错误;
③点H与点A重合时,设BF=x,则AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,即42+x2=(8-x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,故③正确;
④如图,过点F作FM⊥AD于M,
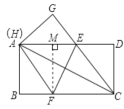
则ME=(8-3)-3=2,
由勾股定理得,EF=![]() ,故④正确;
,故④正确;
综上所述,结论正确的有①③④,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AB=26,AD=6,将□ABCD绕点A旋转,当点D的对应点D′落在AB边上时,点C的对应点C′恰好与点B、C在同一直线上,则此时△C′D′B的面积为()

A.120B.240C.260D.480
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场的打折活动规定:凡在本商场购物,可转动转盘一次,如图,并根据所转结果付账.

(1)分别求出打九折,打八折的概率;
(2)求不打折的概率;
(3)小红和小明分别购买了价值200元的商品,活动后一共付钱360元,求他俩获得优惠的情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长:中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表

组别
海选成绩x
A组
50≤x<60
B组
60≤x<70
C组
70≤x<80
D组
80≤x<90
E组
90≤x<100
请根据所给信息,解答下列问题
①图1条形统计图中D组人数有多少?
②在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角的度数为 度;
③规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.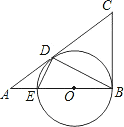
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一台灯示意图,其中灯头连接杆DE始终和桌面FG平行,灯脚AB始终和桌面FG垂直,

(1)当∠EDC=∠DCB=120°时,求∠CBA;
(2)连杆BC、CD可以绕着B、C和D进行旋转,灯头E始终在D左侧,设∠EDC,∠DCB,∠CBA的度数分别为α,β,γ,请画出示意图,并直接写出示意图中α,β,γ之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,求⊙O的半径.

相关试题

