搜索
【题目】古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
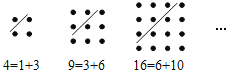
A.13＝3+10B.25＝9+16C.36＝15+21D.49＝18+31
参考答案：
【答案】C
【解析】
本题考查探究、归纳的数学思想方法．题中明确指出：任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．由于“正方形数”为两个“三角形数”之和，正方形数可以用代数式表示为：（n+1）2，两个三角形数分别表示为
n（n+1）和（n+1）（n+2），所以由正方形数可以推得n的值，然后求得三角形数的值．
∵A中13不是“正方形数”；选项B、D中等式右侧并不是两个相邻“三角形数”之和．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（ ）
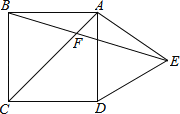
A. 75°B. 60°C. 55°D. 45°
-
科目： 来源： 题型：
查看答案和解析>>【题目】某书店准备购进甲、乙两种图书共100本，购书款不高于2224元，预这100本图书全部售完的利润不低于1100元，两种图书的进价、售价如表所示：
甲种图书
乙种图书
进价（元/本）
16
28
售价（元/本）
26
40
请回答下列问题：
（1）书店有多少种进书方案？
（2）在这批图书全部售出的条件下，（1）中的哪种方案利润最大？最大利润是多少？（请你用所学的函数知识来解决）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市质量技术监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
（1）若标准质量为450克，则抽样检测的20袋食品的总质量为多少克？
（2）若该种食品的合格标准为450±5g，求该食品的抽样检测的合格率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）
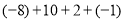
（2）
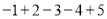
（3）
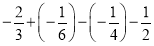
（4）
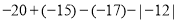
（5）
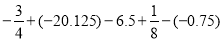
（6）
-
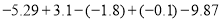
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的三个顶点分别为A（1，2），B（1，3），C（3，1）．若反比例函数y=
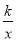在第一象限内的图象与△ABC有公共点，则k的取值范围是（ ）
A. 2≤k≤3B. 2≤k≤4C. 3≤k≤4D. 2≤k≤3.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.
（1）求证：CE＝AD；
（2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
（3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．
相关试题
