【题目】如果P 是正方形ABCD 内的一点,且满足∠APB+∠DPC=180°,那么称点P 是正方形 ABCD 的“对补点”.
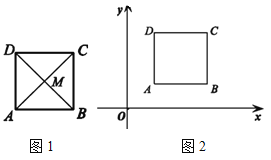
(1)如图1,正方形ABCD 的对角线AC,BD 交于点M,求证:点M 是正方形ABCD 的对补点;
(2)如图2,在平面直角坐标系中,正方形ABCD 的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.
参考答案:
【答案】(1)证明见解析;
(2)对补点如:N(![]() ,
, ![]() ).证明见解析
).证明见解析
【解析】试题分析:(1)根据正方形的对角线互相垂直,得到∠DMC=∠AMB=90°,从而得到点M是正方形ABCD的对补点.(2) 在直线y=x(1<x<3)或直线y=-x+4(1<x<3)上
除(2,2)外的任意点均可,通过证明△DCN≌△BCN,得到∠CND=∠CNB,利用邻补角的性质即可得出结论.
试题解析:
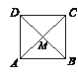
(1)
∵四边形ABCD是正方形,
∴ AC⊥BD.
∴ ∠DMC=∠AMB=90°.
即 ∠DMC+∠AMB=180°.
∴ 点M是正方形ABCD的对补点.
(2)对补点如:N(![]() ,
, ![]() ).
).
说明:在直线y=x(1<x<3)或直线y=-x+4(1<x<3)上
除(2,2)外的任意点均可.
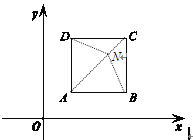
证明(方法一):
连接AC ,BD
由(1)得此时对角线的交点为(2,2).
设直线AC的解析式为:y=kx+b,
把点A(1,1),C(3,3)分别代入,
可求得直线AC的解析式为:y=x.
则点N(![]() ,
, ![]() )是直线AC上除对角线交点外的一点,且在正方形ABCD内.
)是直线AC上除对角线交点外的一点,且在正方形ABCD内.
连接AC,DN,BN,
∵ 四边形ABCD是正方形,
∴ DC=BC,∠DCN=∠BCN.
又∵ CN=CN,
∴ △DCN≌△BCN.
∴ ∠CND=∠CNB.
∵ ∠CNB+∠ANB=180°,
∴ ∠CND+∠ANB=180°.
∴ 点N是正方形ABCD的对补点.
证明(方法二):
连接AC ,BD,
由(1)得此时对角线的交点为(2,2).
设点N是线段AC上的一点(端点A,C及对角线交点除外),
连接AC,DN,BN,
∵ 四边形ABCD是正方形,
∴ DC=BC,∠DCN=∠BCN.
又∵ CN=CN,
∴ △DCN≌△BCN.
∴ ∠CND=∠CNB.
∵ ∠CNB+∠ANB=180°,
∴ ∠CND+∠ANB=180°.
∴ 点N是正方形ABCD除对角线交点外的补点.
设直线AC的解析式为:y=kx+b,
把点A(1,1),C(3,3)分别代入,可求得直线AC的解析式为:y=x.
在1<x<3范围内,任取一点均为该正方形的对补点,如N(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是半圆O的直径,点C在半圆O上.
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是
 的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由. 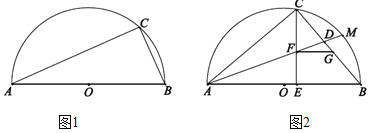
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+(2m+1)x+(m﹣1)=0的根的情况是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
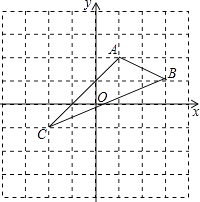
(1)在图中作出△ABC关于y轴对称的△A1B1C1 .
(2)写出A1 , B1 , C1的坐标(直接写出答案),
A1 ;B1 ;C1 .
(3)△A1B1C1的面积为 . -
科目: 来源: 题型:
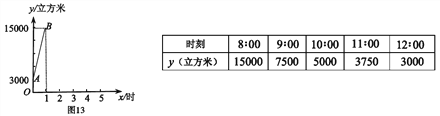
查看答案和解析>>【题目】为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00, 燃气公司给该城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气. 储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
(1)在7:00-8:00 范围内,y 随x的变化情况如图13 所示,求y 关于x 的函数解析式;
(2)在8:00-12:00 范围内,y 的变化情况如下表所示,请写出一个符合表格中数据的y 关于x 的函数解析式,依此函数解析式,判断上午9:05 到9:20 能否完成加气950 立方米的任务,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,a﹣b=5,则代数式a2﹣b2的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队10名队员的年龄结构如表,已知该队队员年龄的中位数为21.5,则x=_____.
年龄
19
20
21
22
24
26
人数
1
1
x
y
2
1
相关试题

