【题目】已知AB是半圆O的直径,点C在半圆O上.
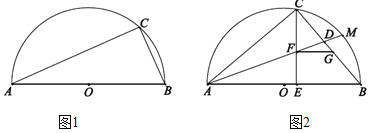
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是![]() 的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
参考答案:
【答案】(1)半圆O的半径为![]() ;
;
(2)⊙D与直线AC相切,理由见解析
【解析】试题分析:(1)依据直径所对的圆周角是直角可得∠C=90°,2再依据三角函数即可求解;(2) 依据△ACE与△CEB相似证出∠AEC=∠CEB=90°, 再依据M是![]() 的中点,证明CF=CD, 过点F作FP∥GB交于AB于点P, 证出△ACF≌△APF,得出CF=FP,再证四边形FPBG是平行四边形,得到 FP=GB从而CD=GB,点D到直线AC的距离为线段CD的长.
的中点,证明CF=CD, 过点F作FP∥GB交于AB于点P, 证出△ACF≌△APF,得出CF=FP,再证四边形FPBG是平行四边形,得到 FP=GB从而CD=GB,点D到直线AC的距离为线段CD的长.
试题解析:
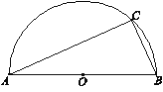
(1)∵ AB是半圆O的直径,
∴ ∠C=90°.
在Rt△ACB中,AB=![]()
=![]()
=2![]() .
.
∴ OA=![]()
(2)
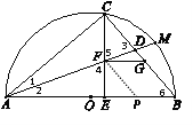
⊙D与直线AC相切.
理由如下:
由(1)得∠ACB=90°.
∵ ∠AEC=∠ECB+∠6,
∴ ∠AEC>∠ECB,∠AEC>∠6.
∵ △ACE与△CEB相似,
∴ ∠AEC=∠CEB=90°.
在Rt△ACD,Rt△AEF中分别有
∠1+∠3=90°,∠2+∠4=90°.
∵ M是![]() 的中点,
的中点,
∴ ∠COM=∠BOM.
∴ ∠1=∠2,
∴ ∠3=∠4.
∵ ∠4=∠5,
∴ ∠3=∠5.
∴ CF=CD.
过点F作FP∥GB交于AB于点P,则∠FPE=∠6.
在Rt△AEC,Rt△ACB中分别有
∠CAE+∠ACE=90°,∠CAE+∠6=90°.
∴ ∠ACE=∠6=∠FPE.
又∵ ∠1=∠2,AF=AF,
∴ △ACF≌△APF.
∴ CF=FP.
∵ FP∥GB,FG∥AB,
∴ 四边形FPBG是平行四边形.
∴ FP=GB.
∴ CD=GB.
∵ CD⊥AC,
∴ 点D到直线AC
∴ ⊙D与直线AC相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=
 BC.
BC. 
(1)用尺规作图的方法,过E点作EF⊥DC,垂足是点F;(不写作法,保留作图痕迹)
(2)求证:DF=CF. -
科目: 来源: 题型:
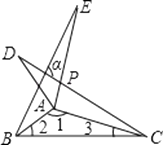
查看答案和解析>>【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( )
A.80°
B.100°
C.60°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
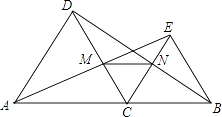
(1)求证:AE=BD;
(2)求证:MN∥AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+(2m+1)x+(m﹣1)=0的根的情况是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
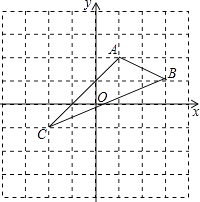
(1)在图中作出△ABC关于y轴对称的△A1B1C1 .
(2)写出A1 , B1 , C1的坐标(直接写出答案),
A1 ;B1 ;C1 .
(3)△A1B1C1的面积为 . -
科目: 来源: 题型:
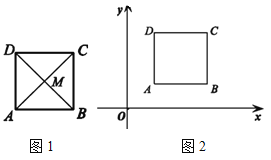
查看答案和解析>>【题目】如果P 是正方形ABCD 内的一点,且满足∠APB+∠DPC=180°,那么称点P 是正方形 ABCD 的“对补点”.
(1)如图1,正方形ABCD 的对角线AC,BD 交于点M,求证:点M 是正方形ABCD 的对补点;
(2)如图2,在平面直角坐标系中,正方形ABCD 的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.
相关试题

