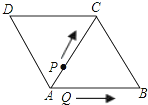
【题目】如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动。设P、Q运动的时间为t秒
(1)当t=2时,PQ=___;
(2)求点P、Q从出发到相遇所用的时间;
(3)当t取何值时,△APQ是等边三角形;请说明理由.
参考答案:
【答案】(1)![]() ;(2)t=4;(3)t=
;(2)t=4;(3)t=![]() .
.
【解析】
(1)、先求出AP,AQ的长度,再根据等边三角形的性质得到△APQ为直角三角形,利用勾股定理即可解答;(2)、△ABC是等边三角形,边长是2厘米.点P、Q从出发到相遇,即两人所走的路程的和是6cm.设从出发到相遇所用的时间是t秒.列方程就可以求出时间;(3)、当P在AC上,Q在AB上时,AP≠AQ,则一定不是等边三角形,当△APQ是等边三角形时,Q一定在边CD上,P一定在边CB上,若△APQ是等边三角形,则CP=DQ,根据这个相等关系,就可以得到一个关于t的方程,就可以得到t的值.
(1)、当t=2时,AP=2×0.5=1厘米,AQ=2×1=2厘米,
如图1,
∵△ABC是边长为2厘米的等边三角形,∴PQ⊥AC,∴PQ=![]() ;
;
(2)、由0.5t+t=6, 解得t=4.
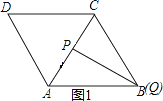
(3)、当0t4时,都不存在;
当4<t6时,如图2,若△APQ是等边三角形,
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP,则CP=DQ,即6t=0.5t2,解得:t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
∠AOB=60°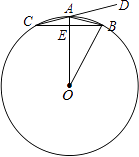
(1)求∠AOB的度数;
(2)若AE=1,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】飞机着陆后滑行的距离S(单位:m)关于滑行时间t(单位:s)的函数解析式是:S=60t﹣1.5t2
(1)直接指出飞机着陆时的速度;
(2)直接指出t的取值范围;
(3)画出函数S的图象并指出飞机着陆后滑行多远才能停下来?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6cm的等边三角形,点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动,与此同时,点E从线段BC的某个端点出发,以b cm/s速度在线段BC上运动,当D到达A点后,D、E运动停止,运动时间为t(秒)
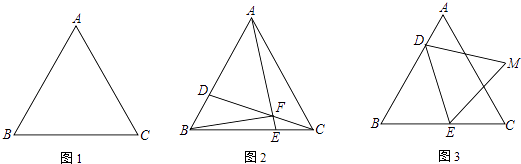
(1)如图1,若a=b=1,点E从C出发沿C→B方向运动,连AE、CD,AE、CD交于F,连BF.当0<t<6时:
①求∠AFC的度数;
②求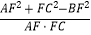 的值;
的值;
(2)如图2,若a=1,b=2,点E从B点出发沿B→C方向运动,E点到达C点后再沿C→B方向运动.当t≥3时,连DE,以DE为边作等边△DEM,使M、B在DE两侧,求M点所经历的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0,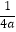 ),准线l:
),准线l: 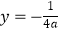 ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0,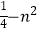 )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
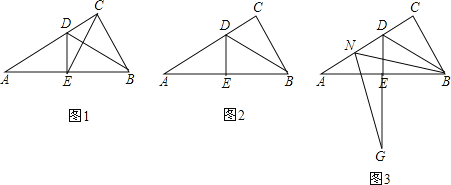
-
科目: 来源: 题型:
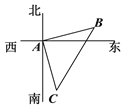
查看答案和解析>>【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1
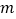 ).
).
相关试题

