【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. 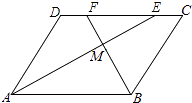
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
参考答案:
【答案】
(1)解:方法一:如图①,
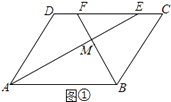
∵在ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
方法二:如图②,延长BC、AE相交于点P,
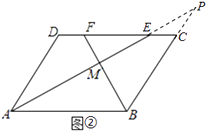
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴AB=BP.
∵BF平分∠ABP,
∴AP⊥BF,
即AE⊥BF
(2)解:方法一:线段DF与CE是相等关系,即DF=CE,
∵在ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.
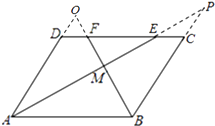
方法二:如图,延长BC、AE设交于点P,延长AD、BF相交于点O,
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴BP=AB.
同理可得,AO=AB.
∴AO=BP.
∵在ABCD中,AD=BC,
∴OD=PC.
又∵在ABCD中,DC∥AB,
∴△ODF∽△OAB,△PCE∽△PBA.
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
∴DF=CE.
【解析】(1)因为AE,BF分别是∠DAB,∠ABC的角平分线,那么就有∠MAB= ![]() ∠DAB,∠MBA=
∠DAB,∠MBA= ![]() ∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形.
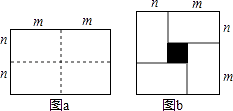
(1)图b中的阴影部分面积为;
(2)观察图b,请你写出三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是;
(3)若x+y=﹣6,xy=2.75,利用(2)提供的等量关系计算x﹣y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(-1,0),A点的横坐标是2,AB=3BC,双曲线
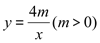 经过A点,双曲线y=-
经过A点,双曲线y=-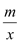 经过C点,则Rt△ABC的面积为_________。
经过C点,则Rt△ABC的面积为_________。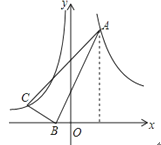
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题是( )
A.半圆(或直径)所对的圆周角是直角
B.对顶角相等
C.四条边相等的四边形是菱形
D.对角线相等的四边形是平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.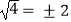
B.(﹣3)3=27
C. =2
=2
D.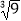 =3
=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已知)
∴∠BFD=∠B(等量代换)
∴AB∥CD()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2﹣14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.
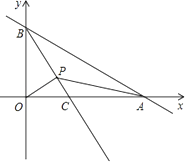
(1)求OA,OB的长;
(2)设△APB和△OPB的面积分别为s1 , s2 , 求s1:s2;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,直接写出时间t;若不可能,请说明理由.
相关试题

