【题目】如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2﹣14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.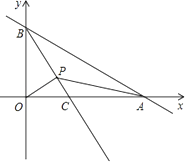
(1)求OA,OB的长;
(2)设△APB和△OPB的面积分别为s1 , s2 , 求s1:s2;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,直接写出时间t;若不可能,请说明理由.
参考答案:
【答案】
(1)
解:∵OA、OB的长是方程x2﹣14x+48=0的两根(OA>OB),
解方程得:x1=8,x2=6,
∵OA>OB,
∴OA=8,OB=6
(2)
解:如图1,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
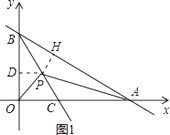
∵BC为∠ABO的平分线,
∴PH=PD,
∴S1:S2=AB:OB,
∵OA=8,OB=6,
∴AB=10,
∴S1:S2=AB:OB=5:3
(3)
解:如图2,过C作CD垂直AB,垂足为D,
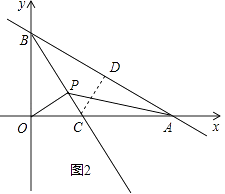
设OC=x,则CD=x,易知BD=OB,
在直角三角形CDA中:CD2+AD2=AC2,
即x2+42=(8﹣x)2,
解得:x=3,
所以C点的坐标(3,0),
∴直线BC的解析式:y=﹣2x+6,
①BP=OB时,t=6,
②BP=OP时,P在OB的中垂线上,yp=3,代入直线BC的解析式得P( ![]() ,3),
,3),
利用勾股定理可得BP= ![]() ,
,
∴t= ![]() ,
,
③OB=OP=6时,设P(m,﹣2m+6),
∴根据勾股定理得:m2+(﹣2m+6)2=62,
解得:m= ![]() ,
,
∴PB= ![]() =
= ![]() ,
,
∴t= ![]() .
.
【解析】(1)解方程x2﹣14x+48=0即可得到结果;(2)根据角平分线的性质得到P是角平分线上的点,P到OB,AB的距离相等,而两个三角形的高相等,S1:S2=AB:OB=5:3;(3)过C作CD垂直AB,垂足为D设OC=x,则CD=x,易知BD=OB,根据勾股定理列方程求得C点的坐标(3,0),得到直线BC的解析式:y=﹣2x+6,然后分三种情况逐一解答①当BP=OB=6时,得到t=6,②点BP=OP时,P在OB的中垂线上,得到yp=3,代入直线BC的解析式得P( ![]() ,3),利用勾股定理可得BP=
,3),利用勾股定理可得BP= ![]() ,即可得到t的值;③当OB=OP=6时,设P(m,﹣2m+6),根据勾股定理列方程m2+(﹣2m+6)2=62 , 解得m=
,即可得到t的值;③当OB=OP=6时,设P(m,﹣2m+6),根据勾股定理列方程m2+(﹣2m+6)2=62 , 解得m= ![]() ,然后再根据勾股定理得到PB=
,然后再根据勾股定理得到PB= ![]() =
= ![]() ,求得结果.
,求得结果.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
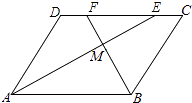
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.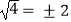
B.(﹣3)3=27
C. =2
=2
D.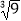 =3
=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已知)
∴∠BFD=∠B(等量代换)
∴AB∥CD()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.

(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级350名学生的视力情况,从中抽查了80名学生的视力.在这个问题中,总体、个体、样本各是什么?上述问题采用的调查方式是普查还是抽样调查?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A、B、C三点在同一条数轴上,其中点A、B对应的数分别为﹣4和1,若BC=3,则AC=_____.
相关试题

