【题目】正方形ABCD的边长为acm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是cm2 . 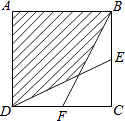
参考答案:
【答案】![]() a2
a2
【解析】解:连接BD,EF. ∵阴影部分的面积=△ABD的面积+△BDG的面积 (G为BF与DE的交点),
∴△ABD的面积= ![]() 正方形ABCD的面积=
正方形ABCD的面积= ![]() a2 .
a2 .
∵△BCD中EF为中位线,
∴EF∥BD,EF= ![]() BD,
BD,
∴△GEF∽△GBD,
∴DG=2GE,
∴△BDE的面积= ![]() △BCD的面积.
△BCD的面积.
∴△BDG的面积= ![]() △BDE的面积=
△BDE的面积= ![]() △BCD的面积=
△BCD的面积= ![]()
![]() a2=
a2= ![]() a2 .
a2 .
∴阴影部分的面积= ![]() a2+
a2+ ![]() a2=
a2= ![]() a2 .
a2 .
故答案为: ![]() a2 .
a2 . 
连接BD,可看出阴影部分的面积等于 ![]() 正方形的面积+一个三角形的面积,用相似求出三角形的面积,阴影部分的面积可证.
正方形的面积+一个三角形的面积,用相似求出三角形的面积,阴影部分的面积可证.
-
科目: 来源: 题型:
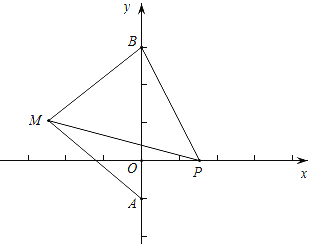
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,﹣1),B(0,3),点M为第二象限内一点,且点M的坐标为(t,1).
(1)请用含t的式子表示△ABM的面积;
(2)当t=﹣2时,在x轴的正半轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
 .其中,正确的结论是( )
.其中,正确的结论是( ) 
A.①②④
B.①③⑤
C.②③④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重 ______ 千克;
(2)这8筐白菜中,最重的与最轻的相差______ 千克;
(3)这8筐白菜一共重多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为 .

相关试题

