【题目】如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为 . 
参考答案:
【答案】10
【解析】解:延长AO交BC于D,作OH⊥BC于H, ∵∠A=∠B=60°,
∴△ABD为等边三角形,
∴∠ADB=60°,AD=BD=AB=6,
∴OD=AD﹣OA=6﹣4=2,
在Rt△ODH中,∠ODH=60°,
∴∠DOH=30°,
∴DH= ![]() OD=1,
OD=1,
∴BH=BD﹣DH=6﹣1=5,
∵OH⊥BC,
∴BC=2BH=10.
故答案为:10.
首先延长AO交BC于D,作OH⊥BC于H,由∠A=∠B=60°,可判断△ABD为等边三角形,根据等边三角形的性质可求得BD的长,再由含30°角的直角三角形的性质,求得DH的长,则可得到BH的长,根据垂径定理的性质,即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为acm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是cm2 .
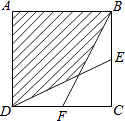
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重 ______ 千克;
(2)这8筐白菜中,最重的与最轻的相差______ 千克;
(3)这8筐白菜一共重多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
相关试题

