Question

【题目】如图，在等腰三角形ABC中，AC=BC，分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE，AE与BD相交于点F，连接CF并延长交AB于点G．求证：CG垂直平分AB．

Answer 1

【答案】证明见解析．

【解析】试题分析：通过证明△AFC≌△CEB可得∠ACF=∠BCF，根据等腰三角形三线合一的性质即可得．

试题解析：∵CA=CB，

∴∠CAB=∠CBA，

∵△AEC和△BCD为等腰直角三角形，

∴∠CAE=∠CBD=45°，∠FAG=∠FBG，

∴∠FAB=∠FBA，

∴AF=BF，

在三角形ACF和△CBF中， ，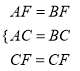

∴△AFC≌△BCF（SSS），

∴∠ACF=∠BCF，

∴AG=BG，CG⊥AB（三线合一），

即CG垂直平分AB.