【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)售价定为90元.利润最大为7500元.
;(3)售价定为90元.利润最大为7500元.
【解析】
(1)当售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件,y=260-x(50≤x≤80),当如果售价超过80元后,若再涨价,则每涨1元每月少卖3件,y=420-3x(80<x<140);
(2)由利润=(售价-成本)×销售量列出函数关系式;
(3)分别求出两个定义域内函数的最大值,然后作比较.
解:![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() .
.
则![]() ;
;
![]() 由利润
由利润![]() (售价-成本)
(售价-成本)![]() 销售量可以列出函数关系式,
销售量可以列出函数关系式,
![]() ,
,
![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
当![]() 有最大值,最大值为
有最大值,最大值为![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,有最大值,最大值为
时,有最大值,最大值为![]() ,
,
故售价定为![]() 元.利润最大为
元.利润最大为![]() 元.
元.
故答案为:(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)售价定为90元.利润最大为7500元.
;(3)售价定为90元.利润最大为7500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形△ABC,直线1过点C且垂直AC.
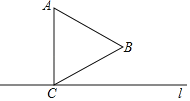
(1)请在直线1上作出点D,使得△ABD的周长最小.
(2)在(1)的条件下,连接AD,BD,求证,AD=2BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个二次函数的图象,三位同学分别说出了它的一些特征:甲:对称轴是
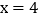 ;乙:与
;乙:与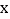 轴两个交点的横坐标都是整数;丙:与
轴两个交点的横坐标都是整数;丙:与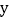 轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为
轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为 .请写出满足上述全部特征的一个二次函数的解析式.
.请写出满足上述全部特征的一个二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
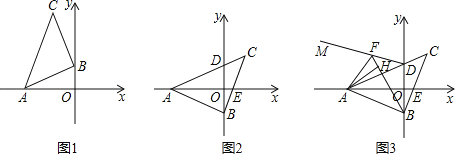
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),点C的坐标为 .
(2)如图2,若OA平分∠BAC,BC与x轴交于点E,若点C纵坐标为m,求AE的长.
(3)如图3,在(2)的条件下,点F在射线DM上,且∠ABF=∠ADF,AH⊥BF于点H,试探究BF、HFDF的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中
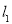 ,
,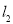 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )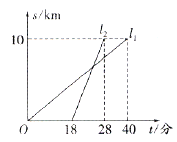
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为
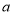 ,较短直角边长为
,较短直角边长为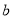 ,若
,若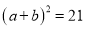 ,大正方形的面积为13,则小正方形的面积为________.
,大正方形的面积为13,则小正方形的面积为________.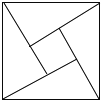
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点
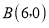 的直线
的直线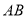 与直线
与直线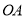 相交于点
相交于点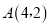 ,动点
,动点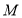 在线段
在线段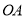 和射线
和射线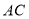 上运动.
上运动.(1)求直线
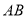 的解析式.
的解析式.(2)求
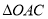 的面积.
的面积.(3)是否存在点
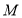 ,使
,使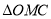 的面积是
的面积是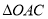 的面积的
的面积的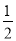 ?若存在求出此时点
?若存在求出此时点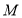 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.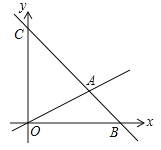
相关试题

