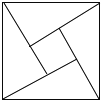
【题目】如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若
,若![]() ,大正方形的面积为13,则小正方形的面积为________.
,大正方形的面积为13,则小正方形的面积为________.
参考答案:
【答案】5
【解析】
观察图形可知,小正方形的面积=大正方形的面积-4个直角三角形的面积,利用已知(a+b)2=21,大正方形的面积为13,可以得出直角三角形的面积,进而求出答案.
解:如图所示:

由题意可知:每个直角三角形面积为![]() ,则四个直角三角形面积为:2ab;大正方形面积为a2+b2=13;小正方形面积为13-2ab
,则四个直角三角形面积为:2ab;大正方形面积为a2+b2=13;小正方形面积为13-2ab
∵(a+b)2=21,
∴a2+2ab+b2=21,
∵大正方形的面积为13,
2ab=21-13=8,
∴小正方形的面积为13-8=5.
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
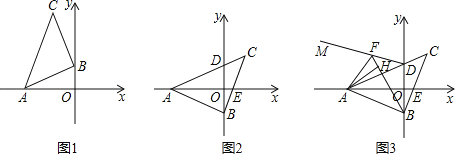
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),点C的坐标为 .
(2)如图2,若OA平分∠BAC,BC与x轴交于点E,若点C纵坐标为m,求AE的长.
(3)如图3,在(2)的条件下,点F在射线DM上,且∠ABF=∠ADF,AH⊥BF于点H,试探究BF、HFDF的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中
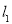 ,
,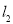 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )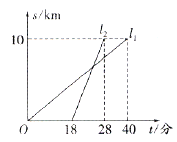
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点
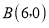 的直线
的直线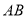 与直线
与直线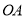 相交于点
相交于点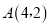 ,动点
,动点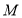 在线段
在线段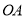 和射线
和射线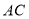 上运动.
上运动.(1)求直线
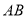 的解析式.
的解析式.(2)求
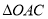 的面积.
的面积.(3)是否存在点
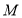 ,使
,使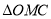 的面积是
的面积是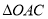 的面积的
的面积的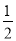 ?若存在求出此时点
?若存在求出此时点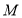 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.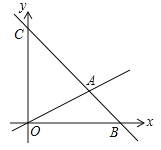
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元)
50
60
70
80
销售数量y(万件)
5.5
5
4.5
4
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
相关试题

