【题目】有一个二次函数的图象,三位同学分别说出了它的一些特征:甲:对称轴是![]() ;乙:与
;乙:与![]() 轴两个交点的横坐标都是整数;丙:与
轴两个交点的横坐标都是整数;丙:与![]() 轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为
轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为![]() .请写出满足上述全部特征的一个二次函数的解析式.
.请写出满足上述全部特征的一个二次函数的解析式.
参考答案:
【答案】![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
根据题意画出图形,直接写出图象与x轴交点的横坐标,根据以这三个点为顶点的三角形面积为3,求出与y轴交点纵坐标,当其值为正数时即可.
解:如图所示:令A点坐标为(3,0),
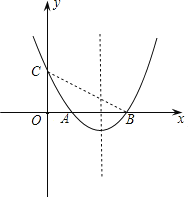
∵对称轴是x=4,
∴B点坐标为(5,0).
又∵△ABC的面积为3,
∴![]() ×AB×OC=3,即
×AB×OC=3,即![]() (5-3)
(5-3)![]() OC=3,解得OC=3,
OC=3,解得OC=3,
∴C点纵坐标为3,是整数,符合题意.
设二次函数解析式为y=a(x-3)(x-5),把C(0,3)代入解析式得:3=a(0-3)(0-5),解得a=![]() ,
,
∴函数解析式为y=![]() (x-3)(x-5),即y=
(x-3)(x-5),即y=![]() .
.
故答案为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
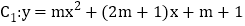 ,其中
,其中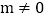 .
. (1)求证:
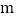 为任意非零实数时,抛物线
为任意非零实数时,抛物线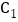 与
与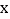 轴总有两个不同的交点;
轴总有两个不同的交点;(2)求抛物线
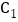 与
与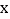 轴的两个交点的坐标(用含
轴的两个交点的坐标(用含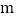 的代数式表示);
的代数式表示); (3)将抛物线
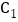 沿
沿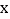 轴正方向平移一个单位长度得到抛物线
轴正方向平移一个单位长度得到抛物线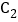 ,则无论
,则无论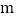 取任何非零实数,
取任何非零实数,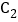 都经过同一个定点,直接写出这个定点的坐标.
都经过同一个定点,直接写出这个定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习过多项式除以单项式,多项式除以多项式一般可用竖式计算,步骤如下:
①把被除式、除式按某个字母作降幂接列,井把所块的项用零补齐;
②用除式的第一项除以除式第一项,得到商式的第一项;
③用商式的一项去乘除式,把积写在被除式下面(同类项对齐),消去相等项;
④把减得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止,被除式=除式×商式+余式,若余式为零,说明这个多项式能被另一个多项式整除.
例如:计算(6x4﹣7x3﹣x2﹣1)÷(2x+1),可用竖式除法如图:

所以6x4﹣7x3﹣x2﹣1除以2x+1,商式为3x3﹣5x2﹣2x﹣1,余式为0.
根据阅读材料,请回答下列问题:
(1)(x3﹣4x2+7x﹣5)÷(x﹣2)的商是 ,余式是 ;
(2)x3﹣x2+ax+b能被x2+2x+2整除,求a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形△ABC,直线1过点C且垂直AC.
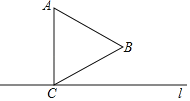
(1)请在直线1上作出点D,使得△ABD的周长最小.
(2)在(1)的条件下,连接AD,BD,求证,AD=2BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
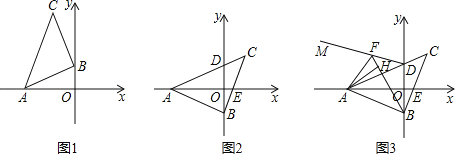
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),点C的坐标为 .
(2)如图2,若OA平分∠BAC,BC与x轴交于点E,若点C纵坐标为m,求AE的长.
(3)如图3,在(2)的条件下,点F在射线DM上,且∠ABF=∠ADF,AH⊥BF于点H,试探究BF、HFDF的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中
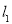 ,
,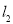 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )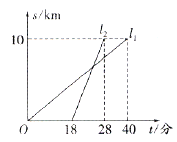
A. 4个B. 3个C. 2个D. 1个
相关试题

