【题目】如图,在Rt△ABC中,∠C=90°,AD=BE=2,点M,P,N分别是DE,BD,AB的中点,则△PMN的周长=___.

参考答案:
【答案】2+![]() .
.
【解析】
先由三角形中位线定理得出PM∥BC,PN∥AC,PM=![]() BE=1,PN=
BE=1,PN=![]() AD=1,再根据平行线的性质得出∠MPD=∠DBC,∠DPN=∠CDB,可证∠MPN=90°,利用勾股定理求出MN=
AD=1,再根据平行线的性质得出∠MPD=∠DBC,∠DPN=∠CDB,可证∠MPN=90°,利用勾股定理求出MN=![]() =
=![]() ,进而得到△PMN的周长.
,进而得到△PMN的周长.
∵点M,P,N分别是DE,BD,AB的中点,AD=BE=2,
∴PM∥BC,PN∥AC,PM=![]() BE=1,PN=
BE=1,PN=![]() AD=1,
AD=1,
∴∠MPD=∠DBC,∠DPN=∠CDB,
∴∠MPD+∠DPN=∠DBC+∠CDB=180°﹣∠C=90°,
即∠MPN=90°,
∴MN=![]() =
=![]() ,
,
∴△PMN的周长=2+![]() .
.
故答案为2+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
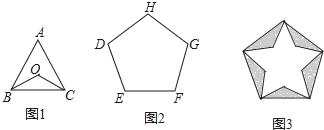
A. 36° B. 42° C. 45° D. 48°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系中放入一个边长AB长为3,BC长为5的矩形纸片ABCD,使得BC、AB所在直线分别与x、y轴重合.将纸片沿着折痕AE翻折后,点D恰好落在x轴上,记为F.

(1)求折痕AE所在直线与x轴交点的坐标;
(2)如图2,过D作DG⊥AF,求DG的长度;
(3)将矩形ABCD水平向右移动n个单位,则点B坐标为(n,0),其中n>0.如图3所示,连接OA,若△OAF是等腰三角形,试求点B的坐标.
-
科目: 来源: 题型:
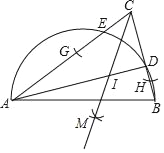
查看答案和解析>>【题目】阅读下面材料:如图,AB是半圆的直径,点D、E在半圆上,且D为弧BE的中点,连接AE、BD并延长,交圆外一点C,按以下步骤作图:
①以点C为圆心,小于BC长为半径画弧,分别交AC、BC于点G、H;
②分别以点G、H为圆心,大于
 GH的长为半径画弧,两弧相交于点M;
GH的长为半径画弧,两弧相交于点M;③作射线CM,交连接A、D两点的线段于点I.
则点I到△ABC各边的距离_____.(填“相等”或“不等”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A顺时针旋转得到△ADE(点B,C的对应点分别是D,E),当点E在BC边上时,连接BD,若∠ABC=30°,∠BDE=10°,求∠EAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2
 ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).
相关试题

